Hypothesis Testing
 |
Your mother, the math teacher, says your fish are getting too big.
She says, "They were on average 70 mm long when you got them. You've been feeding them. They've been growing. They are getting too big for the tank."
|
You say, "No. They are fine. They're still on average 70 mm long."
"Ok. We need more information," said the mother. "One of my former students sold us the fish. He was really into
statistics and wrote some population parameters on the receipt which I kept."
"Your fish tank population mean length was 70 mm, which you already knew. The population standard deviation was 12 mm and
you got about 80 fish."
"Take 36 fish for a sample. Measure them as accurately as you can. We'll assume the population is normal and you can run
a
Hypothesis Test so we can make a judgement based on statistics. Here's a formula for your test statistic. When you finish, we'll see about the fish."

You have no idea what she's talking about!
Before examining how to complete a hypothesis test, examing closely the picture below. Click on the picture to enlarge it.

Old Symbols: - population mean,
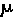 (mu), (mu),
- population standard deviation,
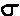 (sigma), (sigma),
- z, the standard normal variable
-
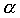 (alpha) - the area under the density function which is not in the confidence interval. (alpha) - the area under the density function which is not in the confidence interval.
Sometimes alpha is in the two tails and other times alpha is only in one tail.
New Symbols: - k-- constant, like 70, ex.
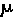 = 70 = 70
- hypothesis (no symbol) -- a theory or statement which may or may not be true
- H0 -- read as "H 0" -- the null (original or beginning) hypothesis
- H1 -- read as "H 1" -- the alternate (new) hypothesis
A hypothesis test is a procedure by which a hypothesis (or statement) which one believes to be
true is tested statistically against another hypothesis already in use.
Before clarification of this, some questions.
- Questions. Swipe between the stars to see the answer.
-
- 1. In the fish tank story, write the tank owner's hypothesis in symbols.
- * H0 = 70*
- 2. In the fish tank story, write the mother's hypothesis in symbols.
- * H1 > 70*
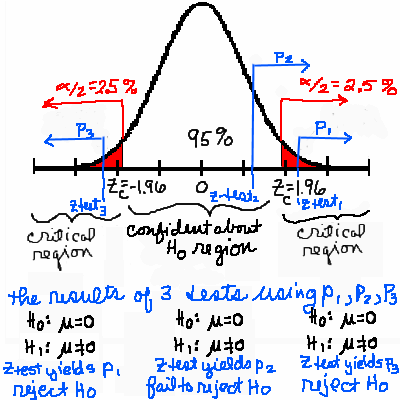
- 3. Will the test be a one-tail test or a two-tail test? *1*
- 4. Use the image
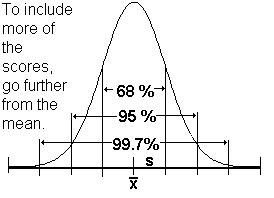
Common confidence intervals which you have seen before.
- Find and state the number that
is labeled zcritical at the 95% confidence level.*zcritical = 1.65*
- 5. Use the image
Common confidence intervals which you have seen before.
- Find and state the number that
is labeled zcritical at the 99% confidence level.*zcritical = 2.58*
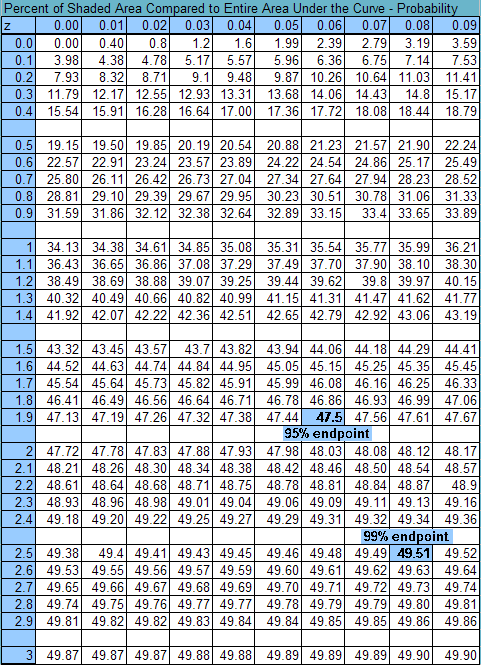
- 6. Where did these zcritical numbers come from before they were put on the image?
- *the table of probabilities given the z-score*
See it.
 | At the left additional z-critical values are listed.
They were also retrieved from the probability table.
|
Here's where we are so far:
- A hypothesis test is
a procedure by which a hypothesis (or statement) which one
believes to be true is tested statistically against another hypothesis already in use. |
- The population is normal.
-
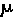 = 70 = 70 -
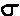 = 12 = 12
- N = 80, approximately
- H0 = 70
- H1 > 70
| -
 - as yet undetermined. - as yet undetermined.
We will use
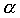 = .01, or 1 % = .01, or 1 %
Level of confidence is 99%.
zcritical = 2.33 - n = 36
- ztest =????
Must compute the ztest

|
The calculator below has been provided to do the computation for you. Please use it to compute ztest.
-
-
- Complete the computation by entering the values and pressing the buttons.
- Enter negative two as "-2."
-
 | As soon as you realize ztest is not
in the confidence interval but out in the tail, the alpha region, larger than the zcritical,
you know it's likely your mother was right, with 99% confidence.
But you could be right.
|
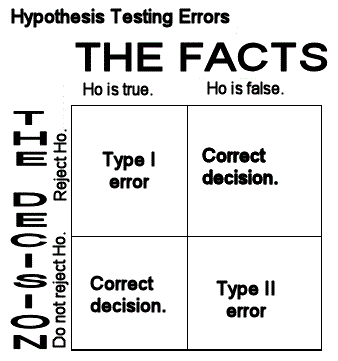 | Thereare two kinds of statistical errors with
a hypothesis test, Type I and type II.
Type II error means "When the null hypothesis is false, you do not reject it."
Type I error means "When the null hypothesis is true, you reject the null hypothesis."
This would be the case if the mean fish length were 70 mm as you believe, but the test results indicate that your mother's hypothesis
that the mean is greater than 70 mm was the one indicated.
|
 | You did not but could have made a math mistake in choosing a
two-tail test rather than the one-tail test you chose for your test.
|
 | Notice on the left a new symbol has been introduced in blue.
It is the "p value," the probability a score is in the extreme of the test statistic.
 |
You can get the p value using either your calculator or
the
Cumulative Standard Normal Distribution.
|
There are many different hypothesis tests because there are many situations
in which new information or verification is desired. We have been looking at a
Z-Test for Normal Density Functions. For additional information on how to run a test see
Hypothesis Testing.
Before continuing, a summary of a test is needed. You need:
 |
- a reason to run the test.
Perhaps, you believe a mean is incorrect,
you think that two means or two probabilities (as in "70% of males," vs "42% of females") are different, ...
- specific information about the situation.
- to decide if a one-tailed or two-tailed test is needed.
- to compute a test statistic.
- to compute either zcritical or a p value.
- to make a decision about your hypothesis.
|
Now, examine other
hypothesis tests the web page, or,
HYPOTHESIS TESTS pdf file or
video about the HYPOTHESIS TESTS pdf file, yes, a video about a pdf file, filed with other videos.
You have completed "A Year of Statistics in an Hour or Two." Stay safe. --A2
Vocabulary
- k-- constant, like 70, ex.
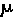 = 70 = 70
- HYPOTHESIS (no symbol) -- a theory or statement which may or may not be true
- HYPOTHESIS TEST - a procedure by which a hypothesis (or statement) which one believes to be
true is tested statistically against another hypothesis already in use.
- NULL HYPOTHESIS - H0 -- read as "H 0" -- the null (original or beginning) hypothesis
- ALTERNATE HYPOTHESIS - H1 -- read as "H 1" -- the alternate (new) hypothesis
- ONE-TAIL TEST - used when the alternate hypothesis, H1, is
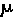
 k, where k is the null hypothesis mean. k, where k is the null hypothesis mean.
- TWO-TAIL TEST - used when the alternate hypothesis, H1, is
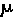 > k or > k or
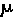 < k, where k is the null hypothesis mean. < k, where k is the null hypothesis mean.
- Z-CRITICAL - zcritical -- the boundary value(s) which end the confidence interval.
- Z-TEST -- the evidence used to accept or reject the null hypothesis, usually computed from sample data.

- TYPE I ERROR - "When the null hypothesis is true, you reject the null hypothesis."
- TYPE II ERROR - -- "When the null hypothesis is false, you do not reject it."
- P VALUE - the probability a score is in the extreme of the test statistic.

Just
vocabulary. |
 A Year of Statistics in an Hour or Two:
A Year of Statistics in an Hour or Two: 
 Population, Sample, Data, Statistic
Population, Sample, Data, Statistic

 Discrete or Continuous
Discrete or Continuous

 Take a Samples
Take a Samples

 Look at the Data
Look at the Data

 Theoretical vs Experimental & Descriptive
Theoretical vs Experimental & Descriptive
 Probability
Probability

 More Vocabulary and Topics that Are Not Included on this Page
More Vocabulary and Topics that Are Not Included on this Page

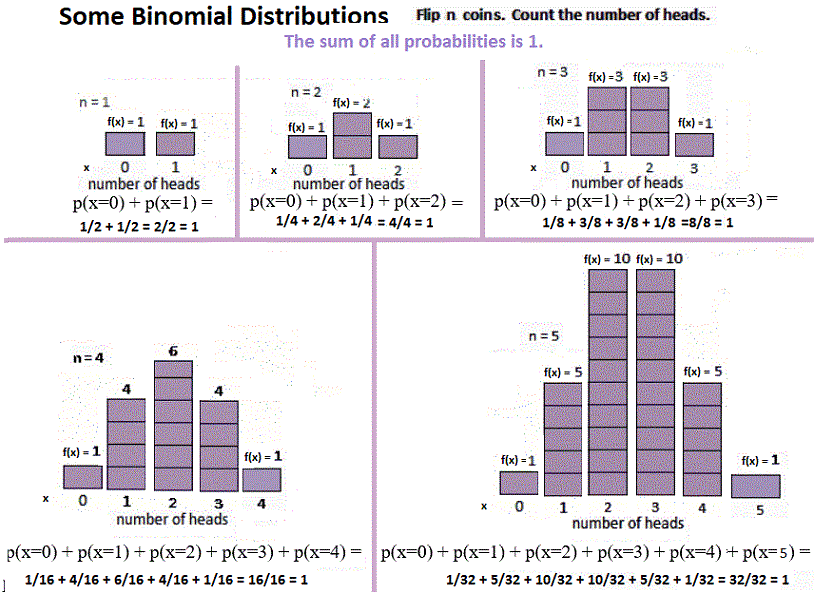
 The Binomial Distribution
The Binomial Distribution

 Thank Goodness for Probability Density Functions
Thank Goodness for Probability Density Functions

 Normal and Standard Normal Distributions
Normal and Standard Normal Distributions

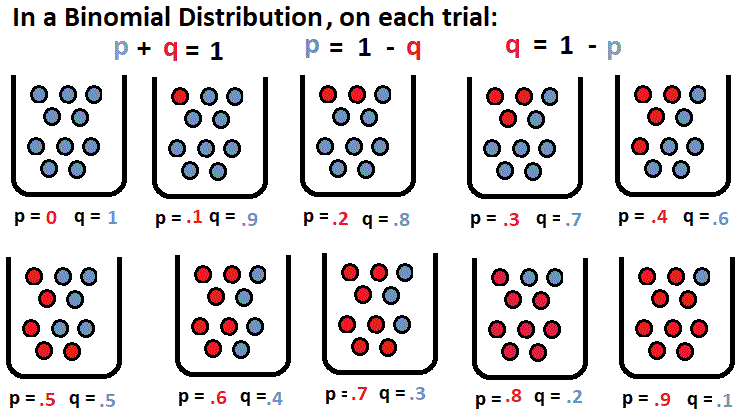
 Confidence Intervals
Confidence Intervals

 Hypothesis Testing
Hypothesis Testing

 Just the Vocabulary (Sorted Alphabetically)
Just the Vocabulary (Sorted Alphabetically)





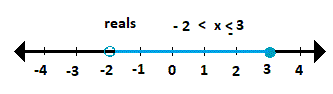







 - a math symbol meaning "add up the terms."
- a math symbol meaning "add up the terms."
 , read as "x bar" - arithmetic average. Formula:
, read as "x bar" - arithmetic average. Formula: 
 , read as "x hat" --median, Q2, the 50th percentile, the middle data point when the data is ordered
from lowest to highest
, read as "x hat" --median, Q2, the 50th percentile, the middle data point when the data is ordered
from lowest to highest
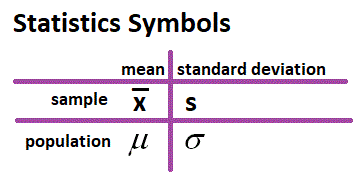







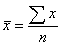 , the arithmetic average, the sum of the numbers divided by the number of numbers.
, the arithmetic average, the sum of the numbers divided by the number of numbers.
 =
= 





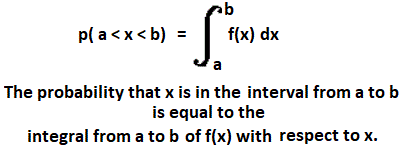

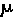 ,
,
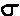 ).
). . This is needed because there are really a whole family of normal distributions, each with their own mean and
standard deviation, but having the same features.
. This is needed because there are really a whole family of normal distributions, each with their own mean and
standard deviation, but having the same features.





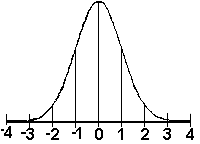







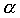 (alpha) - the area under the density function which is not in the confidence interval.
(alpha) - the area under the density function which is not in the confidence interval.











 k, where k is the null hypothesis mean.
k, where k is the null hypothesis mean.
![[MC,i. Home]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
![[Table]](http://www.mathnstuff.com/math/spoken/here/1gif/table.gif)
![[Words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)
![[this semester's schedule w/links]](http://www.mathnstuff.com/gif/semestr.gif)
![[Good Stuff -- free & valuable resources]](http://www.mathnstuff.com/gif/goods.gif)