Sign Test
- This is really a binomial (+ or - response) test to see if evidence exists that a median is the
hypothesized median (single sample) or to see if a difference exists in paired data. If n is less than 26,
a formula is not used, just a count and compare procedure. If n is greater than 25, a z-test is used.
In either case, the smaller of the number of data points above the median and number of data points
below the mean is used to compute the test statistic.
- Needed:
- a sample of 100 to do the job a sample of 30 does w/a more efficient test
- may be nonparametric (not defined mean, standard deviation, etc.)
- random sample
- use the raw data to find the "sign" of [(data)-(stated median)]
- Compute each [(data)-(stated median)] or [(After)-(Before)] first to determine n = x+ + x- !!!
| The null hypothesis always: |
| | H0: median = (stated median) | or | H0: (After) - (Before) = 0 |
| The alternate hypothesis is always one of these: |
| | H1: median < (stated median) | | H1: (After) - (Before) < 0 |
| | H1: median = (stated median) | | H1: (After) - (Before) = 0 |
| | H1: median > (stated median) | | H1: (After) - (Before) > 0 | |
- Test statistic:
| | When n < 26, n = sum of x+ and x- | or | When n > 25, n = sum of x+ and x- |
| | smaller of:
x+, the # of data points greater than median (or 0)
and
x-, the # of data points less than the median (or 0) | | 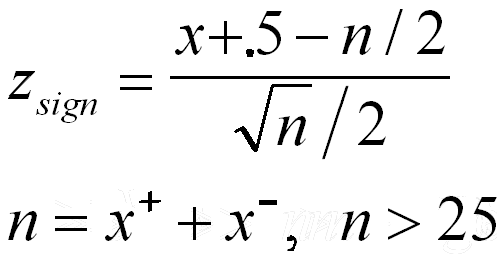 |
| | binomial distribution used where p=.5,
n = the sum of x+ and x-. | |
The z table is used with x in formula as
the smaller x+ and x-. |
- One page Summary , sample problem, and a
spreadsheet.
Wilcoxon Rank Sum Test
- This tests to see if evidence exists that 2 distributions are the same by virtue of
their symmetry, center, and the distribution of ranks (with averaged ranks awarded
to tied data points). Do two populations have the same distribution, are their centers
and spreads the same?
- Needed:
- 2 not necessarily normal distributions
- each sample size is 10 or greater
- independent random samples
- The null hypothesis is always:
- H0: The distributions are the same.
- (The means and rank sums are "the same.")
- Some alternate hypothesis are:
- H1: The distributions are not the same.
- Are the means and rank sums close but not "the same?" (
 ) )
- H1: The first distributions is to the left of the other.
- Is the first's rank sums much smaller, data points more to the left, than the second's? ( < )
- H1: The first distributions is to the right of the same.
- Is the first's rank sums much larger, data points more to the right, than the second's? ( > )
- Test statistic: The sample size determines the labels in the formulas.
- The label n1 is given to the smaller sample size -- fewer numbers to add.
- The data is then POOLED, with averaged ranks awarded to tied data points.
- Individual r1 and r2 are computed by adding the ranks of the data points from the samples.
- R is r1, the sum of the ranks of the sample with the smaller sample size.
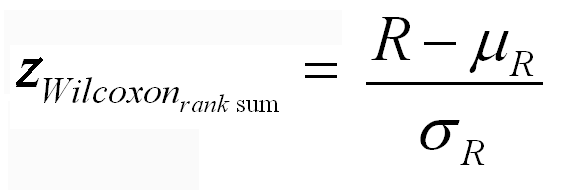 
- One page Summary , sample problem, and a
spreadsheet.
|
Wilcoxon Signed-Rank Test
- This tests to see if evidence exists that the medians of two distributions
- are the same, or before-after differences exist.
- Needed:
- n samples paired as x1 - x2 = difference
 0. 0.
- the ranks of the pooled absolute values of the differences, tie ranks averaged.
- "signed-rank" products = (original sign)(pooled rank)
- the absolute value of the sum of the products of the
- (original sign)(pooled rank) of the negative differences.
- the absolute value of the sum of the products of the
- (original sign)(pooled rank) of the positive differences.
- the SMALLER of the absolute values of the sums of the + or - signed-rank products
- 2 not necessarily normal distributions
- independent random samples
- The null hypothesis is always:
- H0: median1 = median2, or H0: before - after = 0
- Some alternate hypothesis are:
- H1: median1
 median2, or H1: before - after median2, or H1: before - after  0 0
- H1: median1 > median2, or H1: before - after > 0
- H1: median1 < median2, or H1: before - after < 0
- Test statistic:
- if n < 30, use table for critical value and the SMALLER for the test statistic
- if n > 30, use z distribution for critical value and formula
-
with µ = n(n+1)/4 for test statistic OR
- if n > 30, use z distribution for critical value and
- the absolute value of the sum of all (sign)(rank) in formula
- with µ = .5 for test statistic
 
- One page Summary , sample problem, and a
spreadsheet.
|
Spearman rank correlation coefficient

Kruskal-Wallis test

|

-
-
-
![[MC,i. Home]](//www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
![[Good Stuff]](//www.mathnstuff.com/gif/goods.gif)


![[Words]](//www.mathnstuff.com/math/spoken/here/1gif/words.gif)
- © 8/2012 A. Azzolino
- www.mathnstuff.com/math/spoken/here/2class/90/htest2.htm
|
|
 2 Test for A Single Variance
2 Test for A Single Variance  2 Test for Independence of Proportions
2 Test for Independence of Proportions
 2 Test for Homogeneity of Proportions
2 Test for Homogeneity of Proportions
 2 Goodness of Fit Test
2 Goodness of Fit Test
 2 Test for Normality
2 Test for Normality



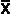 - µ)/(
- µ)/( /
/ (n))
(n))

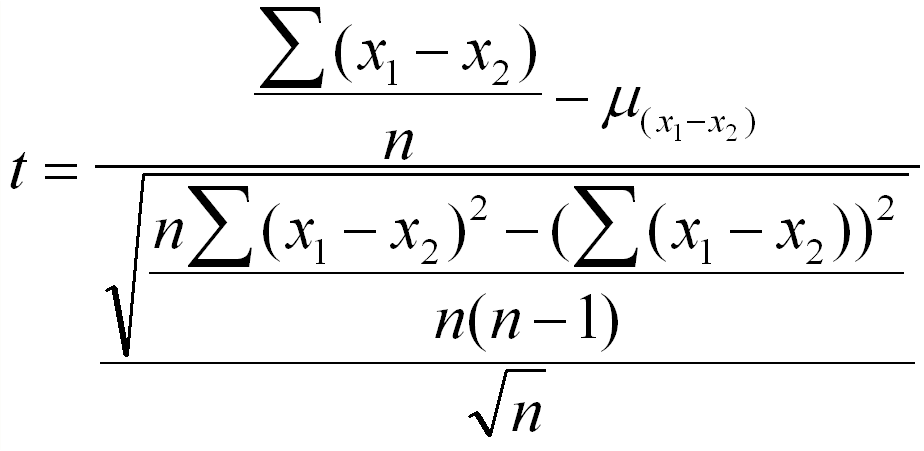






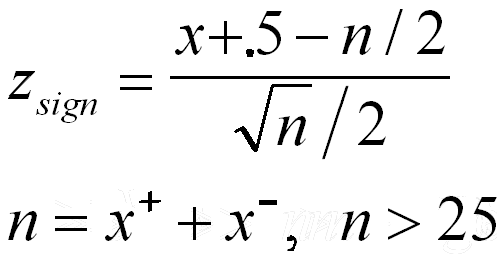
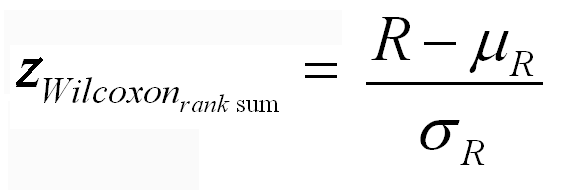


 = x/n, the sample proportion
= x/n, the sample proportion

 (stated proportion)
(stated proportion)  , is the strength of the linear relationship between x and y.
, is the strength of the linear relationship between x and y.







 2cdf( in a program
2cdf( in a program








![[MC,i. Home]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
![[Good Stuff]](http://www.mathnstuff.com/gif/goods.gif)

![[Words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)