Answers
- 1. 3: 3 is the median,
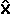 , of 2 and 4. It exactly in the middle of 2 and 4. , of 2 and 4. It exactly in the middle of 2 and 4. -
- 2. 2: there is no other number between the two 2s
-
- 3. 3: 3 is the median,
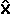 , of 1 and 5. It exactly in the middle of 1 and 5. , of 1 and 5. It exactly in the middle of 1 and 5.
- Notice that 3 is the median of 1-2-3-4-5. Three is the mean of 1 and 5, the mean must be used because there are only 2 numbers.
(1+5)/2 = 3
-
- 4. 3: order the numbers 1, 5
 1*3*5, 3 is in the middle, the median position; 1*3*5, 3 is in the middle, the median position;
- (1+5)/2 = 3: the median,
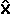 , is 3, is also the mean, , is 3, is also the mean, 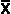 , of 1 and 5 , of 1 and 5-
- 5. 3: because 3 , 7, 2 is 3 numbers the median is easy to find. Order the numbers,
 2, 3, 7 , 2, 3, 7 ,
 is 3 is 3 -
- 6. 2: 0, 4, 0, 4,
 0,0,4,4, 0,0,4,4,  is the mean of the middle 0 and 4 is 2 is the mean of the middle 0 and 4 is 2 -
- 7. 4: 1, 3, 5, 4, 2, 6, 5
 1, 2, 3, 4, 5, 5, 6. 1, 2, 3, 4, 5, 5, 6. - There are an odd number of data points, the median is visible in the ordered middle position.
- The median is 4.
-
- 8. 3.5: 1, 3, 5, 4, 3, 2, 6, 5
 1, 2, 3, 3, 4, 5, 5, 6, the median is 3.5 the mean of 3 and 4 1, 2, 3, 3, 4, 5, 5, 6, the median is 3.5 the mean of 3 and 4 -
- 9. 3: 3 occurs most
-
- 10. 5, 7: 5 and 7 have the highest and equal frequencies, they are each considered modes.
- It is a special case. The sample is said to be bimodal, having 2 modes.
-
- 11. There is no mode because each data point occurs with the same frequency.
-
- 12. 4.5: (2+4+5+7)/4 = 18/4 = 4.5
-
- 13. 2: (1+2+3)/3 = 6/3 =2. Notice, the mean is also the median.
-
- 14. 79%: (100+90+50+75+80)/5 = 395/5 = 79%
-
- 15.
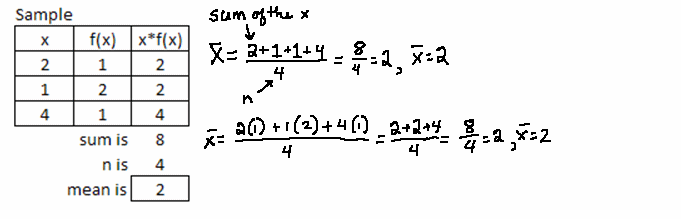 -
- 16. 3.5: 2 is the lo. 5 is the hi. (2+5)/2 = 3.5 Notice it is close to the median which is 4
- and the mean which is 3 2/3.
-
- 17.
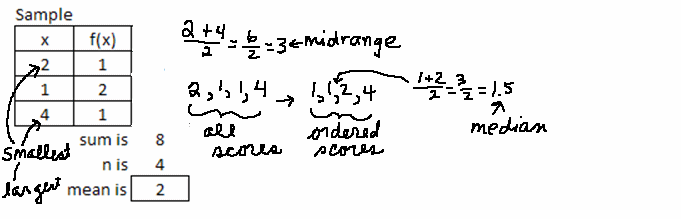 -
- 18. There are 9 data points in the sample. The mean is 8, the mode is 12, the median is 7, and the midrange is 10.5.
The scores range from a low of 1 to a high of 20. The mode has a frequency of 2.
- One might also add: "The data points are:
1, 2, 4, 5, 7, 9, 12, 12, and 20," but this is not usually included.
|





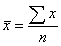 . More Info
. More Info
 answer
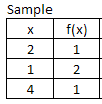
answer  - the arithmetic average - the
sum of the data points divided by the number of data points
- the arithmetic average - the
sum of the data points divided by the number of data points
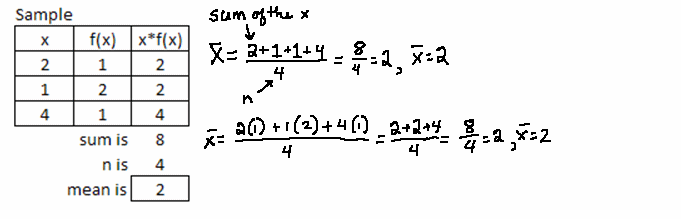
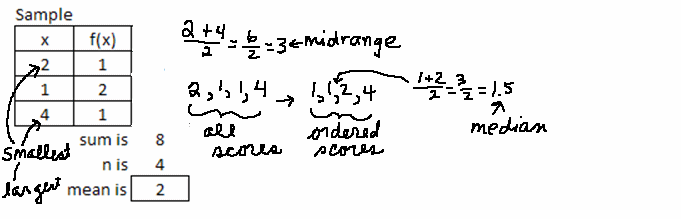
![[MC,i. Home]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
![[Good Stuff]](http://www.mathnstuff.com/gif/goods.gif)
![[Words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)