[tutorials & resource material arranged by topic Class Table [next] [last]

MIDDLE GROUND - Use the Standard Normal to
Compute Probabilities of Normal Distributions


From The Standard Normal Number Line to
Any Normal Number Line to
Probabilities
 
      There exists a normal distribution with a mean of 0 and a standard deviation of 1. It is called the standard normal distribution.
    It is often used to:
  • compare two or more distributions of data.
  • estimate or to compute probabilities of events involving normal distributions.
      The standard normal distribution and scale may be thought of as a tool to scale up or down another normal distribution. The standard normal distribution is a tool to translate a normal distribution into numbers which may be used to learn more information about the set of data than was originally known.
 
      For this kind of work, some standard normal scores (z), the normal distribution mean (either or µ), the normal distribution standard deviation, (either s or ), and the normal distribution scores (x), are required.
 
      Two formulas, stating the relationships between variables, exist to facilitate this work,
            and     .
 
      Compare the formula for x with each of the scale numbers on the "Statistical sample number line," above.
 
      Take the same formula for x, and use some simple algebra to solve for z.
 
 
Given 3 Values, Compute x or z
 
Compute z
 
      Compute a few values of z and then x.
 
      To compute z enter values of x, , and s, then complete the computation by pressing the buttons.

      The formula to compute z:

Enter negative two as "-2."
      score, x:
      mean, :
      standard deviation, s:

      the mean from the score.

      the (x - ) by s to obtain z:
Compute x
 
 
      To compute x enter values of z, , and s, then complete the computation by pressing the buttons.

      The formula to compute x:

Enter negative two as "-2."
      z-score, z:
      mean, :
      standard deviation, s:

      the z-score and standard deviation.

      + zs to obtain x:
 
 
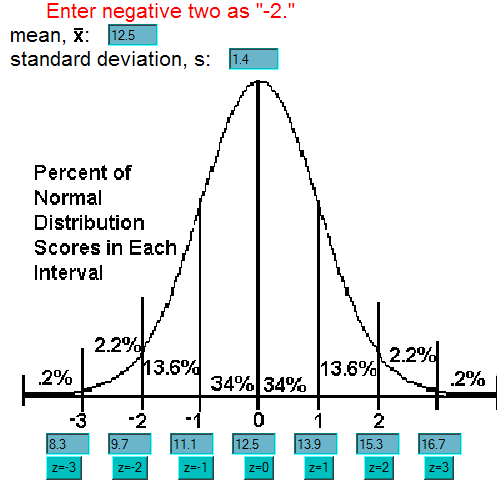
Compute the scale for the normal distribution
to see how the data looks
 
      This part of the page is designed to decrease arithmetic.
      Enter the mean and standard deviation.   The page will compute the scale values, then, you may use the page to help complete the problems below.
      If the input boxes below do not line up with the scale on the graphic, use your browser's VIEW Text Size to adjust the text size so things do line up.
 
      Enter negative two as "-2."
mean, :  
standard deviation, s:  
                 
                                 
      You now how the ability to
  • compute a normal distribution score, x, given the desired z-score, mean, and standard deviation,
  • compute a standard normal score, z, given the desired x-score, mean, and standard deviation,
  • create a number line scale to get an good idea how the data is distributed,
  • compute an exact probability for numbers that happen to fall on certain scale, standard deviation, values.
      Now on to the problems.
 
 
Between, Below, Above

      There are 3 basic types of probability problems dealing with distributions, including normal and standard normal distributions. They are summarized by the words between, below, and above. Figure out which kind of problem you have and the computation becomes easy.
 
      In addition to this page which completes computation so you may verify your work, blank statistics paper has been provided.
 
      Below, a sample problem is completed w/the page & w/paper.
      Of course, sometimes the desired area may not be computed directly.
 
      Addition or subtraction of two areas many be required to find the desired area or percent or probability.

 
 
Example
      State the probability a score, from data which is normally distributed, falls within 2 standard deviations of the mean given a mean of 12.5 and a standard deviation of 1.4.
 
 
Use Information on This Page
to Answer These Questions
 
1. Complete: The mean of the standard normal distributions is ___.
 
2. Complete: The standard deviation of the standard normal distributions is ___.
 
3. Given a normal distribution with a mean of 75.4 and a standard deviation of 12.32,
a. estimate p(50 < x < 88)      
b. p(x > 63)
c. p(x < 100)
 
4. State the z-score which matches a score of 12.6 from a normal distribution given the mean is 10 1/2 and the standard deviation is 1.25.
 
5. State the probability a score is greater than 25 if the distribution is normal, the mean is 20, and the standard deviation is 5.   Show pencil & paper work.
 
6. Terry and Tony each got an 88 on stat tests but they were different but equivalent tests. The teachers were willing to state the mean and standard deviation for each test. Below are the statistics. Who got the better grade?
Terry Tony
grade: 88     grade: 88
: 74 : 78
s: 11.2 s: 9.2
 
  answers [next] [last]
[MC,i. Home] [Table] [Words] Classes [this semester's schedule w/links] [Good Stuff -- free & valuable resources] [next] [last]
© 2005, Agnes Azzolino
www.mathnstuff.com/math/spoken/here/2class/90/standrd.htm