-
Never Certain
-
- Before reading this section review the good news
The Data Is Centered About the Mean-Mode-Median, then, get ready for the bad news.
-
-
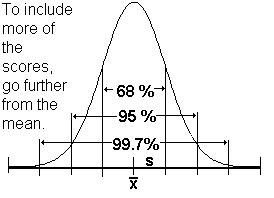
-
- The bad news is one is never certain where the data will fall. Though the normal distribution data is centered
about the mean, one can't tell for certain if a specific score will be close to the mean or far from the mean.
-
- It doesn't matter what kind of things the scores are: raw scores, x, with a mean of
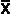 , or sample means, , or sample means,
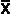 , with a population mean of µ. One can not be certain, but, for a two-tail test these distribution of scores are very
useful. , with a population mean of µ. One can not be certain, but, for a two-tail test these distribution of scores are very
useful.
-
- Because 68% of normally distributed scores fall within one standard deviation of the mean, one might expect 68%
of the scores drawn at a certain time to be within 1 standard deviation of the mean, but this is not guaranteed. One is never certain, but one can be 68% certain
about the decision made on a two-tailed hypothesis test if this useful information is used.
-
- If we wished to have a 68% confidence level about our hypothesis test, we would go one standard deviation from the
mean,
z-scores from -1 to 1. See change the scale.
-
- If we wished to have approximately a 95% confidence level,
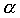 at 5%, about out hypothesis test, we would go
two standard deviation from the mean, z-scores from -2 to 2. at 5%, about out hypothesis test, we would go
two standard deviation from the mean, z-scores from -2 to 2.
-
- It is important to note that even if at 95% confidence level, 5% of the scores will fall outside this
confidence interval and this is expected and the reason one says, "Statistics means never having to say you are certain." More on that later.
-
- If we wished to have approximately a 99.7% confidence level about out hypothesis test, we would go
three standard deviation from the mean, z-scores from -3 to 3.
-
- More exact intervals are listed below organized by
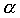 , alpha. , alpha.
-

-
- The above table of z-scores, used as critical scores, means if we wished to have 99% confidence in
our test results on a two-tailed test, we'd go 2.58 standard deviation from the mean, z-scores from -2.58 to 2.58.
-
- If the score falls in this interval, we do not reject the null hypothesis. If the score falls outside the
confidence interval, in either of the critical intervals greater than 2.58 or less than -2.58, we can with 99% confidence reject the null hypothesis.
-
- Again recall, even at 99% confident, there is still the possibility of a decision error, the topic of a later section.
|

![[MC,i. Home]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
![[Table]](http://www.mathnstuff.com/math/spoken/here/1gif/table.gif)
![[Words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)

![[this semester's schedule w/links]](http://www.mathnstuff.com/gif/semestr.gif)
![[Good Stuff -- free & valuable resources]](http://www.mathnstuff.com/gif/goods.gif)
![[last]](http://www.mathnstuff.com/math/spoken/here/1gif/last.gif)
![[next]](http://www.mathnstuff.com/math/spoken/here/1gif/next.gif)



![[MC,i. Home]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
![[Table]](http://www.mathnstuff.com/math/spoken/here/1gif/table.gif)
![[Words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)

![[this semester's schedule w/links]](http://www.mathnstuff.com/gif/semestr.gif)
![[Good Stuff -- free & valuable resources]](http://www.mathnstuff.com/gif/goods.gif)
![[last]](http://www.mathnstuff.com/math/spoken/here/1gif/last.gif)
![[next]](http://www.mathnstuff.com/math/spoken/here/1gif/next.gif)