The Languages of the Math Classroom

16. object

The internet can not provide an example of concrete mathematics, the best it can do is provide a pictorial representation of the concrete. But, in mathematics some "things" are not even objects. Mathematics is often said to be abstract rather than concrete for just this reason, many mathematical "things" are not objects.

Communication is further hampered between those speaking the mother tongue and those speaking the purest form of formal mathematics because the meaning in one language is not the same as the meaning in the other language!

Consider the mathematical "things" called function and triangle.

Examples: Function and Triangle

A function is an abstraction and not an object. One can't see or touch it. It's a certain performance described by a rule or the verbal or, more informally, the written expression of that performance or occurance, or, again more informally, the symbolic coding for the performance, or the graphic representation of that idea/rule/phenomena. Mathematically, it's a performance of a very special nature, but, it's not an object.

Those speaking only the mother tongue might say they do not know what a function is in mathematics.

Those speaking only the mother tongue might say they do have knowledge of what a triangle is in mathematics.

A triangle is an abstraction in formal mathematics and an object in the mother tongue. It may be a three-sided polygon, a drawing or paper representation of this idea, or a three dimensional object constructed of straws which "looks like" a triangle. Formal mathematics would consider the last two cases models of triangles because they describe or mimic the properties of triangles, but they are not the abstract mathematical "object" a triangle.

Usually, the context may clarify whether a "thing" in mathematics is strictly a mathematical idea or an object or both.

Teaching Strategy: Speak both "Mother Tongue" and "Formal Mathematics"

Again, I recommend, one speaks both the mother tongue and formal mathematics. Speak of the formal mathematics triangle - a 3-sided polygon - made of points and line segments, things which can be thought but not humanly created, but which may be represented or modeled through a drawing. Speak also of the figure the triangle which clearly can be drawn on paper which is still a mathematical "object" and a more concrete version of the abstract formal mathematics "object."

---

17. model

In both the mother tongue and formal mathematics a model is a replica or a smaller version of a "thing" which has some or all of the properties of the "thing" it models. In formal mathematics, a model is often an equation used to describe a performance or situation, as in the above example of function, the equation was a more concrete representation of the function. In formal mathematics, as discussed above, the model might not even be a thing you can hold because you can't hold a function or equation.

Example: Slope

Slope is a mathematical "object," an abstract one.

Slope is the rate of change of the function with respect to the change in the variable. It is in informal mathematics "rise over run." More concretely, it is the tilt of the curve. As an equation:

Most often it is stated as a number and symbolized by the lower case letter "m."

The Slopemeter © models even more concretely the idea of slope and what the number represents.

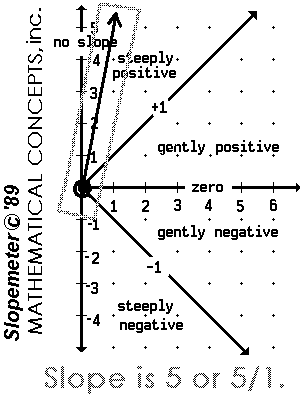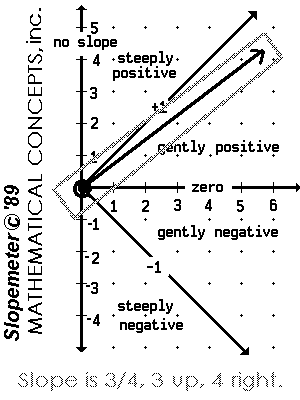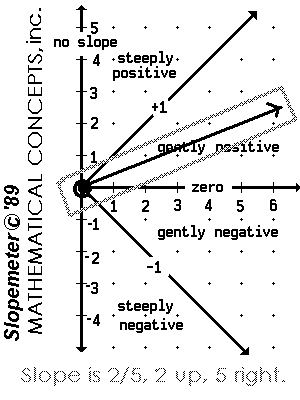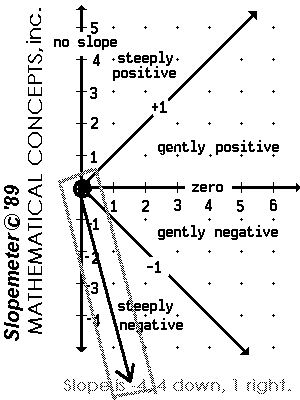
The Slopemeter © is a slope gauge.

Placed on the graph of a function, it can be used to measure its slope. The arm of the Slopemeter is a ray with an end point at a point of tangency. It models slope in that slope is a measureable quantity and may be determined through the use of a tangent line or ray.

Teaching Strategy: Permit Free Play Before Structured Work

Whenever possible, permit free play before any formal use of an object, manipulative, or model.

The free play permits the user to begin to use the mother tongue in order to create a vocabulary and the tactile use permits verbs to "form" before they are introduced formally.

---

18. manipulative/token

The concrete language of manipulatives and token really can't be demonstrated on a web page. The closest it can come is through animated gifs to pictorially present a representation of the tokens being placed to create the communication desired.

The reader is asked to take two detours. First jump to the Hundreds Board to explore the mathematical language of the manipulative or token to represent counting numbers and their addition before continuing on the representations below.

[Once there, you may jump back to this spot in the text to continue.]

Then jump to the Graphing With Manipulatives to explore the mathematical language of the manipulative or token in representing functions before continuing on to the representations below.

[Once there, you may jump back to this spot in the text to continue.]

---

Dilation

Below on the left, multiples of a number, the dilation of a constant by each of the natural numbers, is represented by placement on the 100s board.

Below on the right, all multiples of a number are represented by placing a line on the coordinate plane. To a nonuser of Graphing with Manipulatives, it looks like the pictorial language graph. To a user of Graphing with Manipulatives, it recalls how the manipulatives are used to communicate concretely.

Example: Dilation in two formats: The Hundreds Board and Coordinate Plane.

Dilation is a "thing" in mathematics. It is an expansion or contraction of some nature. In the real world, cameras and eyes open and close, they dilate, in order to control the amount of light utilized.

The picture below is the closest this page comes to duplicating the use of manipulatives or tokens to model the concept of dilation of "a number" by a constant.

Teaching Strategy: Permit free play before structured work.

I know, I know, I said that before. But, it is worth repeating.

---

References

• Exploring Functions through the Use of Manipulatives

  © 9/16/94, Agnes Azzolino, TXu-660-820, ISBN 0-9623593-3-5 and

  © 7/30/91, Graphing with Manipulatives Agnes Azzolino, TXu-490-556, ISBN 0-9623593-2-7

• MATH SPOKEN HERE!

  "perimeter," page P:16-3.

  © 1/13/87, Agnes Azzolino, TX 2 020 938 and

  © 8/29/95, Agnes Azzolino, TX 4-140-039

---

[Table of Contents] [Top of the Page] [Last Page] [Next Page]
[Verbal] [Written] [Pictorial] [Concrete]

---

The Languages of the Math Classroom

    Verbal, Written, Pictorial, and Concrete (the Hundreds Board, for example) are the four broad mathematics language families discussed in this electronic monograph found at www.mathnstuff.com/papers/langu/page0.htm and additional pages (ISBN: 1-929-870-01-9 © 1998, Agnes Azzolino).

© 2005, Agnes Azzolino www.mathnstuff.com/math/spoken/here/papers/langu/page9.htm