Earlier, when discussing the families of math classroom languages, the pictorial family was listed as one of the more concrete language groups. The pictorial languages fall into two broad catagories -- those which are more concrete and those which are more symbolic.
The more symbolic pictorial languages include numerals, graphs, maps, things upon which the sender and the receiver have an agreed upon vocabulary. The creation of an accurate picture or graph is not the end of the story unless each of the two communicating understand the picture or graph, for each picture or graph is a codified language in itself.
Blueprints and street maps are found in a math classroom, weather and topological maps usually are not, though each has its own codified language. Two-dimensional coordinate plane graphs are often found in a math classroom. See "A Graph Is a Portrait." Three-dimensional maps are usually not part of the classroom material until calc III.
The more concrete pictorial languages include pictures and movies of "real world" things, drawings and cartoons of "real world" things, things for which the sender and the receiver may not need an agreed upon vocabulary.
The pictorial is often the bridge between the symbolic and the concrete.
![[Top]](//www.mathnstuff.com/gif/top.gif)
13a. moving picture, 13b. static picture


So, what the difference between the moving and static picture as far a communication goes?
In the static picture, the receiver simultaneously receives the beginning, middle, and end of the communication. The receiver has the ability to examine the whole picture or a detail or details. The receiver may spend as much time as desired with the static picture examining the picture and gleaning the message. The receiver can see the whole idea at once and relationships between parts.
In the moving picture, the sender orchestrates the presentation of message, the story line, perhaps even the sound (perhaps a spoken language component). The receiver may have the ability to repeat or replay the picture, but the moving picture is more like a lecture or event or happening.
Teaching Strategy: Use a large picture rather than a small picture.

You "get the picture."
![[Top]](//www.mathnstuff.com/gif/top.gif)
14. graph
The graph or picture is a symbolic representation. Communication is not completed unless:
- a picture or graph is produced,
- each understands the codification of the picture or graph.
Teaching Strategy: Use as many language families as possible.
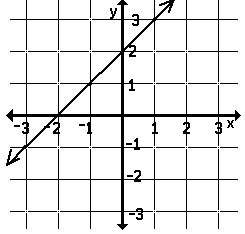
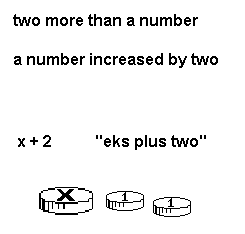
- The graph on the left and the picture of tokens on the bottom right are representatives of exressions in pictorial languages. The written mother tongue and written formal mathematics expressions on the top right are representative of the written language group. The expressions, "x + 2" is written symbolic mathematics. The expression "eks plus two" mimics symbol speak, a verbal language. Each looks/sounds very different. They each mean the same thing.
Teaching Strategy: Use as many language families as possible.
- The expressions, "x + 2" is written symbolic mathematics. The idea
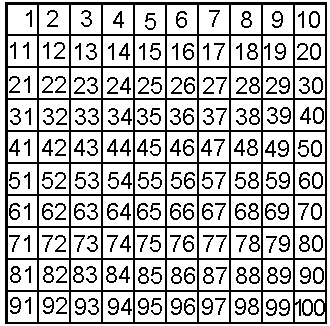
"two more than a number" is also represented in numeral format in the table below.
a number two more than a number 2 4 3 5 4 6 -6 -4 1/2 2 1/2 - "Speak" both languages.
![[Top]](//www.mathnstuff.com/gif/top.gif)
19.numeral
You can tell by the numbering that this language is the "most recent" math language.
Numerals are the figures used to represent a number, 4, 89, and 57, for example. The reader may disagree with the recognition of numeral as a pictorial language and consider it a written symbolic language. If you are in disagreement, complete this short calculator experiment.
Have someone enter a set of functions unknown to you in the y= menu of the calculator then one at a time set the calculator to display the table of numbers with only the x values and the values for each function, one function at a time.
If you can consistently "read" the function from the numerals, you speak this language. If you can not, as many students can not, then you can not "speak this language" or recognize it as a language, and are in the repression stage of numeral linguistics.
You say, "OK. maybe. So what are the verbs of this language?"
The verbs are order, sort, group - anything one does with things and anything one does with groups of numbers. like statistical analysis, pattern recognition.
The importance of the placement of the numeral with the pictorial languages is that it recognizes numeral as a language which is less sophisticated than the written or verbal language groups and more sophisticated than the concrete group.
Consider this last point in defense of this language and its placement. Many people consider a numeral a number. To them, a number is a thing as concrete as a dog or cat. To them, a number is not an idea. They do not speak formal mathematics. Numeral is their concrete and symbolic mathematics language.
![[Top]](//www.mathnstuff.com/gif/top.gif) 15. nonverbal
15. nonverbal
Here's a little quiz - a warmup for the next activity. Each of the figures below is a hand signal, a nonverbal communication, appropriate to a math class. Identify the meaning(s) then DTWYP.
 |  |
 |  |
If your answers were two, concave down, concave up, and horizontal or zero slope, your hand signal linguistics is great. If not, perhaps your partner is willing to coach you.
The next activity requires a bigger commitment on your part. Please stand and get ready to complete your Math Exercises. When you are ready, jump to this page.
![[Top]](http://www.mathnstuff.com/gif/top.gif)


![[MC,i. Home]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
![[Table]](http://www.mathnstuff.com/math/spoken/here/1gif/table.gif)
![[Words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)

![[this semester's schedule w/links]](http://www.mathnstuff.com/gif/semestr.gif)
![[Good Stuff -- free & valuable resources]](http://www.mathnstuff.com/gif/goods.gif)
![[next]](http://www.mathnstuff.com/math/spoken/here/1gif/next.gif)
![[last]](http://www.mathnstuff.com/math/spoken/here/1gif/last.gif)