Binomial Distribution Explained More Slowly

$[tutorials & resource material arranged by topic$ $Class Table$

MIDDLE GROUND - Binomial Distribution Explained More Slowly

I. Brief Summary of A Binomial Distribution
0. Basic Probability and Counting Formulas
Vocabulary, Facts, Count the Ways to Make An Ordered List Or A Group
The average is the sum of the products of the event and the probability of the event.
II. Binomial Distribution Explained More Slowly
III. Binomial Formula Explained
Combinations Compute The Number of Each Outcome in A Binomial Distribution
What's the Probability of Obtaining Exactly 3 Heads If A Fair Coin Is Tossed 4 Times?
Applications
IV. Sum of the Probabilities and the Binomial Mean
The Sum of The Probabilities Is One.
The Expected Value Is The Mean.
The Mean, Expected Value, Is (n)(p).
Why the mean, expected value, is (n)(p)
V. Examples
VI. Use the Normal to Compute the Binomial on a Calculator

A Binomial Distribution, Explained More Slowly

An Action with Only Two Possible Outcomes

Binomial in algebra means the sum of two terms.

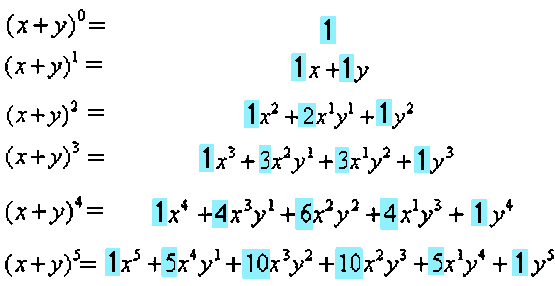
as in the above binomial expansions with Pascal's Triangle highlighted in blue.

Binomial in probability begins with an action, or trial, having only two possible outcomes. The two and only two possible results of the action are success and failure.

Let the probability of a successful outcome of this action be the value p and the probability of failure be the value q. Because the sum of all the probabilities for an experiment is 1 and since there are only two outcomes, p+q=1 and q=1-p.

The action might be as simple as tossing a coin to obtain a head or a tail. One of the outcomes is declared to be a success and the other outcome is declared to be a failure. It doesn't matter which. In the example at the top of the page, obtaining a head on the toss was declared to be a success.

The outcomes need not be equally likely. If the coin is fair, the probability of success, p, is 1/2 and the probability of failure, q, is also 1/2, since, 1/2 + 1/2 = 1, or 1 - 1/2 = 1/2.

If the probability of success in this action, p, is 2/5 or .4, the probability of failure of this action, q, is 1 - 2/5, or .6.

Each Performance of the Action Is Independent
-- Each Trial Is Independent.

Independent -- each trial stands alone.

The result of one trial has no infuence on any other trial.

When a coin is flipped, the outcome is not influenced by the last flip of the coin.

An only two-possible-outcome experiment, repeated a certain number of independent times is called binomial. The distribution or function has as a variable x, the number of successes. The other required parameters are n, the number of independent trials, and p, the probability of success on each trial. The probability of failure on each trial is q, or 1 - p.
Binomial

To be BINOMIAL:

There are n, a specific number, of trials -- n identical actions.

Each trial is independent -- the result of one trial has no effect on another trial.

Each trial has only 2 outcomes -- success or failure.
The probabililty of success on a trail is called p.
P(success) = p.
The probabililty of failure on a trail is called q.
P(failure) = q.
This also means that q = 1 - p and p = 1 - q.

The number of successes in the n trials is the variable.

Once these BINOMIAL conditions are met:

The probability of x successes in n independent trials is given by the formula:

The mean and standard deviation of a binomial distribution are stated below.

A binomial distribution is a discrete, not continuous, distribution. Since x, the variable, is the number of successes in n trials, it can only take on the numbers 0, 1, 2, 3, 4, and so on up to and including n.

$[MC,i. Home]$ $[Table]$ $[Words]$ $Classes$

[Good Stuff -- free & valuable resources]