TI-83 Excel Sketchpad formulas

      MAT123 Spring 2025 Notes

Comments ... A Deck of Playing Cards Hi,       Once upon a time, in 1968, I took probability in college. Many of the male students in the class spent their out of class time in the basement of the student center playing cards. I spent my time in the backstage area of the theatre in the same building, building sets, using power tools, teaching theatre majors how to construct sets. I did not know how to play cards. This lack of experience in playing cards made it difficult in statistics when the prof spoke of the p(4A), the probability of getting 4 aces in a hand, or getting a straight or flush. I knew what aces were but not what a straight or flush was.       In my early days teaching at MCC, in the early 1980s, I taught statistics without having taken a statistics course in college. So, ...       Today I present to you a deck of cards and suggest that the knowledger of a straight or flush might be a good thing to have in your background knowledge even though I will not discuss these topics here.   Go with confidence.   Stay safe, A2

Basic Vocabulary experiment -- an action that is performed event -- a result of an experiment or action, an outcome outcome -- a result of an experiment or action, an event sample space -- the set of all possible outcomes/results/events of an experiment independent event - uninfluenced, stand alone, the result of one stage or trial has no effect on another stage or trial.     ex. Raw sample data - the number of heads when 3 coins are flipped.         The result of each flip, or trial, is not influenced by the other flips. dependent event - having an influence on other stages or trials, the result of one stage of the collection of raw data,         has an effect on another stage.     ex. Raw sample data - the names of a president and vice president of a club with 4 members.         One officer must be picked at a time or you would not know which officer was which.         For instance: There are 4 choices for president, but only 3 choices for vp.         The result of the first stage influences the second stage. with replacement - restore the original conditions after each trial. A after a trial or stage, the setting is restored to the original setting before beginning the next trial or stage.     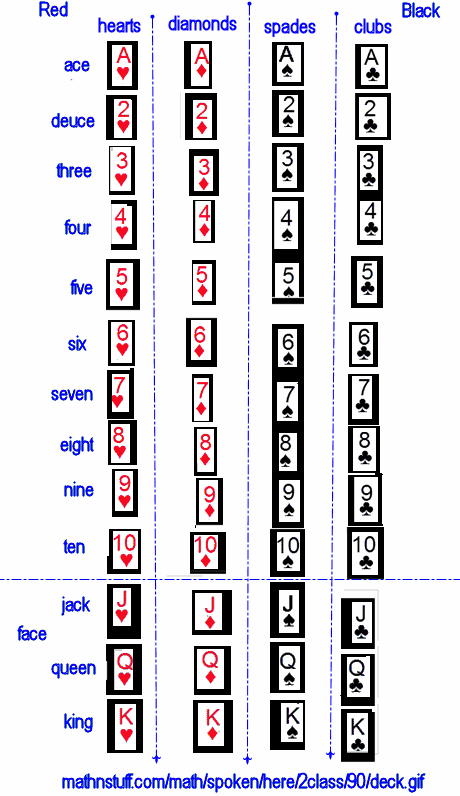ex. Raw sample data - draw a card from a deck, replace the card in the deck, draw a card from the deck. The 2 draws are independent. The replacement made each draw have the same outcomes. without replacement - do not restore the original conditions after each trial, use the new conditions.     ex. Raw sample data - draw a card from a deck, draw a 2nd card from the deck.     Probability probability of an event -- P(event), or p(event)     ex. p(A), the probability of event A     ex. p(head), the probability of obtaining a head     ex. p(x=3), the probability the variable is 3 or the probability of the number 3 occuring, or the probability of obtaining a 3. probability of an event, P(event) = f/n,   (frequency of the event) P(event) =   (number of events in the sample space)   Facts       The lowest possible probability an outcome might have is 0.             If P(event)=0, the event can not happen.       The highest possible probability an outcome might have is 1.             If P(event)=1, the even does happen.       Probabilities range between 0 and 1, inclusive.             0 < P(event) < 1.       The sum of all the probabilities for an experiment is 1.     ex. Experiment: flip a fair coin.             P(head) + P(tail) = 1     ex. Experiment: flip a weighted coin.             P(head) + P(tail) = 1     ex. Experiment: pick a day of the week.             p(Sunday) + p(Monday) + ... + p(Saturday) = 7/7 = 1     ex. Experiment: pick a day of the week             p(January) = 0 Probability in Words, & Symbols, & Computation Words Symbols Computation an event , EVENT E probability of event P(EVENT) P(event) = f/n,   (frequency of the event) P(event) =   (number of events in the sample space) probability of event A P(A) P(A) = f/n,   (frequency of the event A) P(A) =   (number of events in the sample space) probability of event B P(B) P(B) = f/n,   (frequency of the event B) P(event) =   (number of events in the sample space) probability of either event A occurring or event B occurring or both happening -- OR as in a union of outcomes If A and B are mutually exclusive events, then     P(A OR B) = P(A) + P(B), because P(A AND B)= 0 P(A OR B) P(A OR B) = P(A) + P(B) - P(A AND B) probability of both event A and event B occurring -- AND as in the intersection of outcomes P(A AND B) P(A and B) = P(A)P(B) probability of event A happening given that even B has happened         P(A GIVEN B) or P(A|B)         P(A|B) = P(A AND B)/P(B) probability of event B happening given that event A has happened P(B GIVEN A) or P(B|A) P(B|A) = P(A AND B)/P(A) probability of A times the probability of B P(A)P(B)

© 3/15/2025, A2, Agnes Azzolino mathnstuff.com/math/stat/23sp25.9.htm