

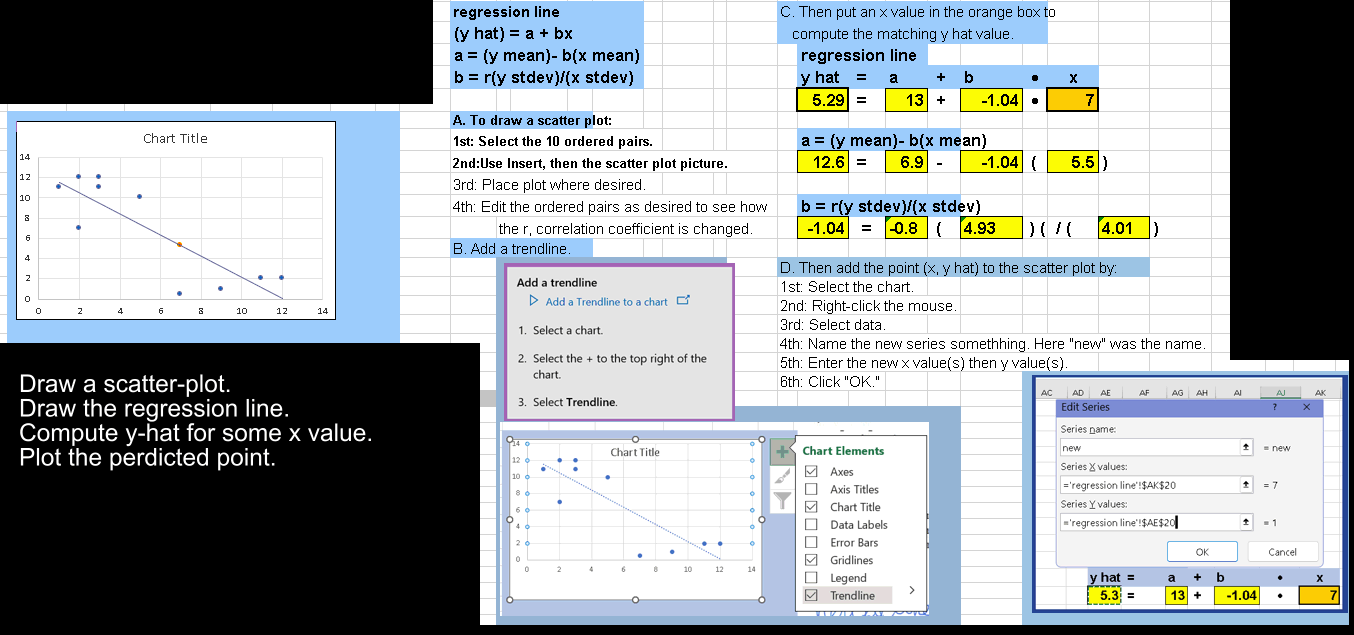
| formulas |
 | ||||||||||
 |
 | |||||||||
| ||||||||||



|
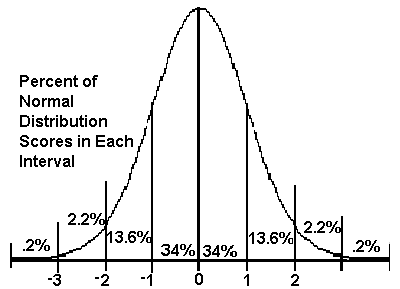
You should already know how to: * use random number generator * use a table to generate a z -score * collect data from the web and store it in a spread sheet * screen capture and place the captured image in a file * rename a file, attach a file to email * compute and interpret 1-variable sample statistics w/a TI and on a spread sheet * compute and interpret 2-variable statistics including correlation coefficient, coefficient of determination w/a TI and on a spread sheet * compute z-scores * use z-scores to determine % of scores above and below the z score and its corresponding x score from a sample |
You also need to know how to: * create a new page in a spread sheet * name a page in a spread sheet * use the self-computing tables to compute sample statistics and z-scores * use the self-computing spread sheet to compute * copy and paste |
Use a correlation coefficient to interpret the regression estimates: For example, suppose: R = .55 → The correlation coefficient is .55. This indicates a _________________ (strength & sign) linear association between x and y. R^2 = (.55)^2 = .3025 → The coefficient of determination is .3025. We can interpret this to mean that about 30% of the variation in y can be explained by the linear relationship with x. About 70% of the variation in y is not explained by the linear relationship with x and is due to other factors. If R^2 = .30 → The coefficient of determination is .3. So, about 30% of the variation in y CAN BE EXPLAINED by the linear relationship with x. And, about 70% of the variation in y CAN NOT BE EXPLAINED by the linear relationship with x and is due to other factors. |
Coefficient of determination, r2 -- the fraction of the variation in y that is explained by least-squares regression of y on [divided by] x. Correlation coefficients whose magnitude are between indicate variables which can be considered 0.9 and 1.0 very highly correlated. 0.7 and 0.9 highly correlated. 0.5 and 0.7 moderately correlated 0.3 and 0.5 low correlation less than 0.3 little if any (linear) correlation Correlation Coefficients at https://www.andrews.edu/ |
|
© 2/21/2025, A2, Agnes Azzolino mathnstuff.com/math/stat/23sp25.8.htm |