
 MAT129 Fall 2024 Notes
MAT129 Fall 2024 Notes
Monday November 18 Topics: Using, Solving, and Verifying Trigonometric Identities
- 9.1 - pg 696, Learning Objectives
- * Verify the fundamental trigonometric identities.
-

- Fundamental Identities
-
Oscar, Unit Circle on 10.30.d.gif
- Cofunction identities
- The function of an angle is equal to the cofunction of its complement.
-
complement on 10.28.a.gif
-
complement, supplement gsp -- just complementary & supplementary angles
- Even-odd Identities
-
picture the graphs of the functions on 11.04.c.gif
- sine and tangent are odd so: f(-x) = - f(x)
- cosine is even so: f(-x) = f(x)
- Reciprocal Identities
11.04.d.gif
- Quotient Identities
- tan(A) = sin(A) / cos(A)
- cot(A) = cos(A) / sin(A)
- oscar
-
similar figures
- Pythagorean Identities
Pythagorean Trig Identities
- sine-cosine, sin2(A) + cos2(A) = 1
pyth1.gif
- tangent-secant, tan2(A) + 1 = sec2(A)
pyth2.gif
- cotangent-cosecant, cot2(A) + 1 = csc2(A)
pyth3.gif
- Unit Circle and Identities
-
unitSinCosTriangle gsp -- sine & cosine functions with a unit circle
-
unitTanSec gsp -- tangent & secant functions with a unit circle
-
unitCotCsc gsp -- cotangent & cosecant functions with a unit circle
-
unitfx gsp -- 6 functions with a unit circle
-
Pythagorean gsp -- using only figure to adjust angle
-
PythagorIdentities gsp -- using either figure or parameter theta to adjust angle
-
- More to Come on Another Day
- Sum and Difference Identities
- Double-Angle Formulas
- Half-Angle formulas
- Reduction Formulas
- Product-to-Sum Formulas
- Sum-to-Product Formulas
-
- * Simplify trigonometric expressions using algebra and the identities.
![[MC,i. Home, site home page]](//www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)




![[Words]](//www.mathnstuff.com/math/spoken/here/1gif/words.gif)


![[Essays]](//www.mathnstuff.com/math/spoken/here/1gif/essay.gif)

![[Table]](//www.mathnstuff.com/math/spoken/here/1gif/table.gif) © 11/17/2024, A2 © 11/17/2024, A2
http://www.mathnstuff.com/math/precalc/129/M.11.18.htm
|



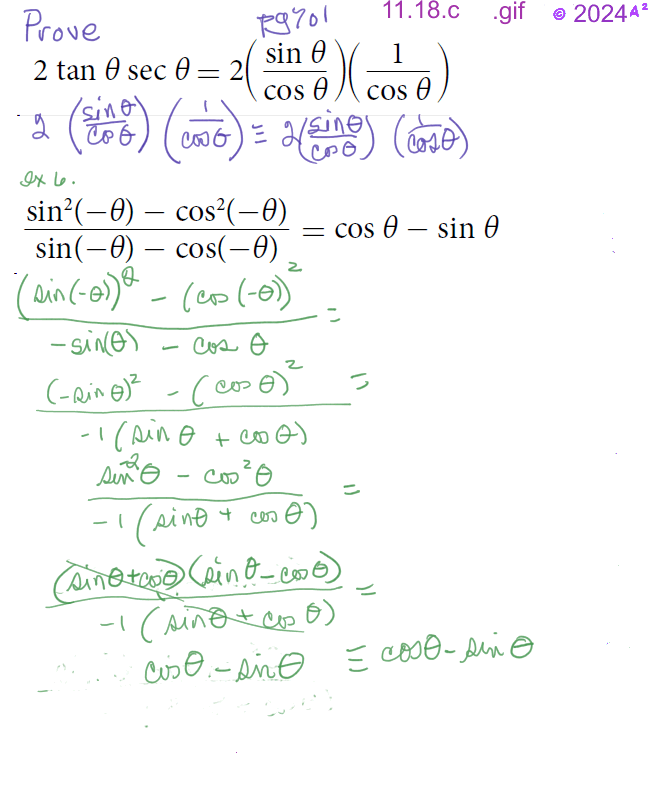




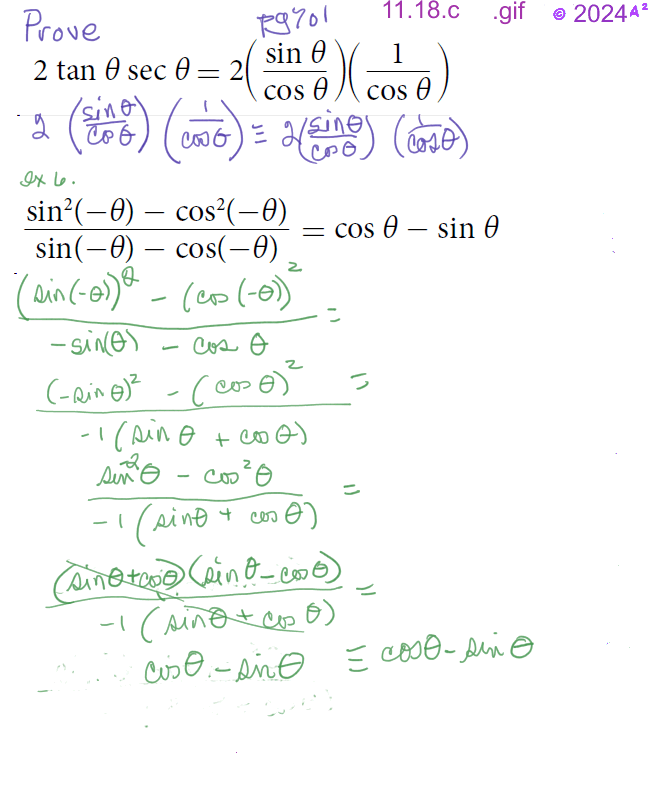

 MAT129 Fall 2024 Notes
MAT129 Fall 2024 Notes