| Cover | cover  |
| Title Page | i  |
| Copyright Page | ii  |
| Dedication | iii  |
| |
| An Overview and Directions | v  |
| Table of Contents | vii  |
| |
| Essential to Every Activity | |
| 0: Speaking, Hearing, and Writing about Functions and their Graphs | 1  |
| 0-1: Describe Graphs: Technical and Creative Perspectives | 1  |
| 0-2: The Identity Function is the Input Function | 2  |
| 0-3a: Describe a Graph by Creating a Wordbank | 2  |
| 0-3b: Supply a Wordbank to Assist in Describing the Graph of Function | 3  |
| 0-4: Present a "Paper" | 3  |
| 0-5: Play 20 Questions | 4  |
| 0-6: "I'm Thinking of a Function" | 5  |
| 4: Visualizing Functions and Graphs | 6  |
| 4-1: Draw a Function in the Air | 6  |
| 4-2: Doing Math "Exercises" | 6  |
| 4-3: Take a Limit with Your Hands | 7  |
| |
| Families of Functions: Translations, Reflections | |
| 11: Addition of Functions, Vertical Slides | 8  |
| 11-1: Vertical Slides | 8  |
| 12: Product of Functions, Reflection about the Horizontal | 11  |
| 12-1: Reflections about a Horizontal Line | 11  |
| 13: Other Compositions of Functions, Horizontal Slides | 13  |
| 13-1: Horizontal Slides or Translations | 13  |
| 14: More Compositions of Functions, Reflections about the Vertical | 15  |
| 14-0: Point-Plotting | 15  |
| 14-1: Discussing the Composition of a Function | 15  |
| 14-2: Reflection about a Vertical Line | 17  |
| |
| Solving Equations and Systems | |
| 15: Solving Systems, Making Statements | 18  |
| 15-1: Using A Graph as a Boundary | 18  |
| 15-2: Solving An Equation Graphically | 19  |
| |
| An Introduction to Functions | |
| 1: Teacher-Lead Point-Plotting of a Function | 23  |
| 1-1: Examine a Function Through Point-Plotting | 23  |
| 2: Student Exploration Using Point-Plotting | 25  |
| 2-1: Discovery by Pairs of Students | 25  |
| 3: Create a Function Poster Library | 28  |
| 3-1: Make a Poster Library | 28  |
| |
| A Closer Look at Functions | |
| 5: The Slope of a Curve at a Point | 31  |
| 5-1: Read Slope from the Slopemeter | 31  |
| 5-2: Read the Slope Using a Tangent to a Curve | 33  |
| 5-3: Computed Slope by the Slope Formula | 34  |
| 5-4: Guessing the Slope of A Function Whose Slope is Computed by Taking the Derivative | 34  |
| |
| 6: Reflections about Y = X | 36  |
| 6-1: Discuss the Differences, Predict the Graph | 36  |
| 6-2: Simple and Mental Reflection about Y=X | 37  |
| 6-3: Manipulatively Finding a Reflection about Y=X | 37  |
| 6-4: Verification through Verbalization and Algebraic Coding | 39  |
| 6-5: Bounding an Area | 39  |
| 7: Inversely So: Finding the Potential Inverse Function | 41  |
| 7-1: The Vertical Line Test | 41  |
| 7-2: The Horizontal Line Test | 42  |
| 7-3: Using Vertical and Horizontal Lines to Ascertain Domain and Range | 42  |
| 7-4: Determining the Inverse Function | 44  |
| 8: Considering the Slope of Inverse Functions | 47  |
| 8-1: Estimating Slopes of Inverse Functions | 47  |
| 8-2: Generalizing about the Slopes of Functions and Their Inverses | 47  |
| 9: Function Values at Neighborhoods and Extremes | 48  |
| 9-1: Function Values in Neighborhoods and at Extremes | 48  |
| 9-2: Consider the Value of the Function in a Neighborhood about a Restricted Value | 50  |
| 9-3: Consider Boring Cases | 51  |
| 10: The Unit Circle | 53  |
| 10-1: Measurement of the Trig Functions of One Angle | 53  |
| 10-2: Generalizing about the Behavior of A Trig Function | 54  |
| 10-3: Pythagorean Identities | 54  |
| The Unit Circle Overhead Model and Activity Sheet | 56  |
| |
| More on Dilation | |
| 16: By a Constant Functions, Making Things Fat and Skinny | 57  |
| 16-1: Comparing Dilations | 58  |
| 16-2: A Project | 58  |
| 17: More Addition of Functions: Polynomials | 60  |
| 17-1: Addition of Functions | 60  |
| 18: More Product of Functions: Rational, Trig Functions, and Envelope Functions | 63  |
| 18-1: Product of Functions [Everyday Functions] | 64  |
| 18-2: Predicting A Graph Based on the Behavior of Related Functions | 68  |
| 18-3: Graphing Nonroutine functions | 70  |
| |
| APPENDIX |
| Table of Contents | A-1  |
| Function and Relation Library | A2  |
| Lines: Vertical and Horizontal lines, Linear Functions | A2  |
| Three Most Important Functions: Identity, Opposite, Reciprocal | A3  |
| Family of Quadratics, Squaring & Square Root, Polynomials, Roots and Exponents | A4  |
| Exponential or Power Functions, A Bit about e, the Exponential Function | A5  |
| Lograthmic Functions, the Natual Log Function, Absolute Value Function Conics | A6  |
| Conics | A7  |
| Trigonometric Functions and the Unit Circle, Trigonometric Functions and the Unit Circle, | A8, A9  |
| Mechanical Manipulatives: Demo Pack and Unit Circle Assembly and Masters | A10 - A14  |
Parent Function Masters: Shapes for 1/x, 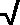 (1 - x²), (1 - x²), 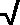 (4 - x²), (4 - x²), 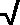 (9 - x²), (9 - x²), | A15  |
halfplane, sine or cosine, not x, x, exp(x) or ln(x), x, ¦x¦, x², and 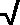 x x | A16 - A19  |
| Additional Function Masters: Shapes for secant or cosecant, tangent or | A20  |
| cotangent, .25x², .5x², 2x², 4x², 10x², .1x², x² and not x², y>x², and y < x², | A21 -A24  |
| not 2x², not 4x², not 10x², and not .1x², not .25x² and not .5x² | A25 - A26  |
| Coordinate Planes: Coordinate Plane Paper, 2 Planes Paper, 4 Planes Paper | A27 - A29  |
| About the Author | A30  |
| |
| Additional Planes | Planes
 |