|
|
what's a model worth? |
|
Manipulative or Model
A model, which the instructor handles, or a manipulative, which the student handles, presents a method of instruction different from traditional lecture, or "chalk and talk." Distance between two points is an ideal topic for such a presentation. This article discusses two different models or manipulatives for use in a classroom or in a lecture hall setting, suggests a decrease in the use of "symbol-speak" and an increase in the use of our more abstract English language, and provides writing-to-learn or critical-thinking-type summary questions. About the ModelThe goal is to concretely represent distance in one-, two-, and three-dimensions. To do this a rectangular box may be used. Corners A, (x1,y1,z1), and B, (x2,y2,z2), represent two points. The sides of the box model distance in one-space -- distance on a line. The diagonal of the base of the box models distance in two-space -- distance on a plane. Using an additional paper plane and the box, one may model distance in three-space. Cut out the paper pieces. Crease then fold back and forth the dashed segments. Folding printed side in, construct the box. Use paper clips or fingers at the narrow ends to hold the box rigid. Examine the printing, the symbols and segments, as the box is constructed and make mathematical statements. 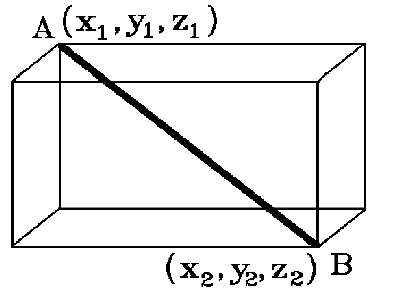
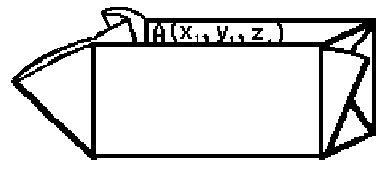
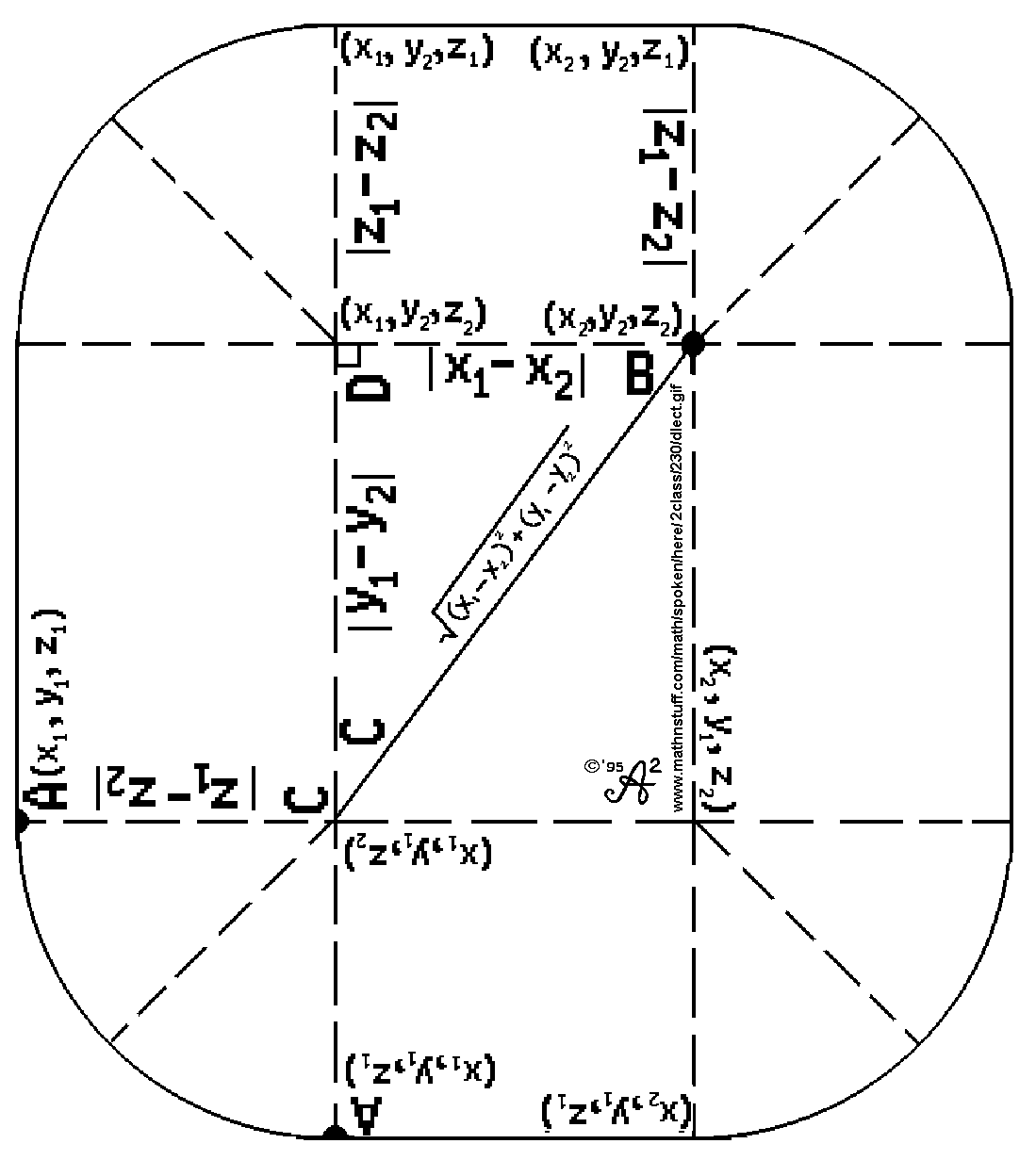
The dimensions of the box, 12 by 8 by 9, employ two sets of Heronian Pythagorean triples, 9-12-15 and 8-15-17, such that the hypotenuse of one triangle is the leg of another triangle. The length of segment (hypotenuse) BC is 15. The length of hypotenuse AB, the modeled distance between two points, is 17. Coordinates of all vertices of the rectangular box are printed on the template. Reference points A, B, C, and D are included to facilitate discussion and to identify triangles ABC and BCD. The length, width, and height of the rectangular box are labeled as the differences in x- coordinates, written |x1-x2|, the difference in y-coordinates, written |y1-y2|, and the difference in z-coordinates, written |z1-z2| . |
The Classroom Model or Manipulative
Copies of the rectangular box might be made of paper or on acetate. If made of paper, students could construct the model then hold it in their hands for examination. If made of acetate, each rectangle in the net should be cut out separately and taped with transparent tape for permanent assembly and prior to use on an overhead projector. |
|
The Lecture Hall Manipulative
The lecture hall manipulative requires additional pre-use work. It also requires yarn to be drawn through the paper and for the yarn to be taped. Paper clips are optional. Steps 1 through 4 below must be completed before use in the lecture hall. 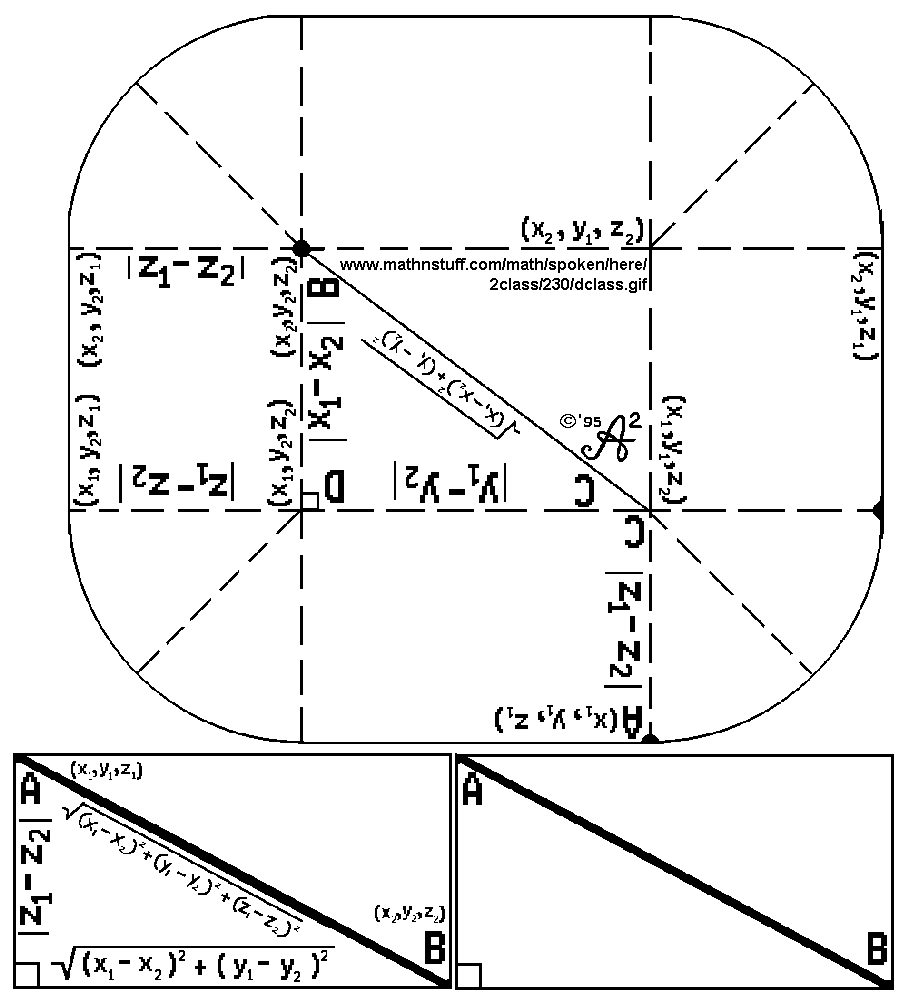
|
|
Discussing the Distances
The model "speaks" concretely. To "speak" symbolically and to "speak" with words, one would need the following expressions, phrases, and sentences. The author encourages this "verbalization" as a necessary part of any manipulative activity. Avoid "symbol speak" by saying the words, not just reading the symbols. The length and width, lengths BD and CD are sides of triangle BCD. The hypotenuse of BCD is segment BC. Its length is the positive square root of sum of the squares of the length and width. 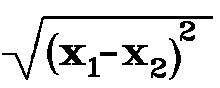
Segment BC is a leg of triangele ABC. The other leg is segment AC, the height, or |z1 - z2| , or the positive difference between the coordinates. The length of the hypotenuse AB is now computable. It is the positive square root of sum of the squares of the height and length BC. 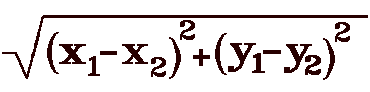
This may be simplified to its usual form. The distance between corners A and B is the positive square root of the sums of the squares of the length, width, and height of the rectangular prism. The distance between (x1, y1, z1) and (x2, y2, z2) is the positive square root of the sums of the squares of the differences in the corresponding coordinates of the points. 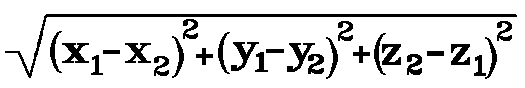
|
|
Summary Activities: From Hand to Head, Then, From Head to Hands
A necessary part of each concrete or manipulative activity should be an more abstract or a written/spoken/summary component. Some sample summary activities follow.
|
|
After Word
The above article, exclusive of the words ", Then, From Head to Hands," was submitted for publication in June 1996, rejected in May 1997, and resubmitted in June 1997, with the following new passage on "chalk and talk vs. concrete thought," and, never published. The new passage introduces an new dimension to the use of manipulatives and concrete thought — reluctance on the part of sincere and knowledgeable professionals. This too is part of manipulative use in education. |
|
"Chalk-and-Talk" vs "Concrete Thought"
If you've reached this point in the article two things are true. The article has finally been published and you might be one of the "choir" who least need "preaching" about the benefits of concrete thought. Reviewers for one journal decided the manuscript was "not suitable for publication." Their comments and the author's responses are stated here in defense of manipulative use. Since reviewers of a professional journal have given these as reasons for the unsuitability of this piece, perhaps the profession needs to hear the reviewers' rational and the author's responses. Reviewer 1:"In the reviewers' experience, students do not seem to have great difficulty with this topic. Heuristic arguments of the sort given in Poly's How to Solve It are effective." Author's Response:Are there no students who have difficulty with this topic? In what context is this statement made? In Algebra I when subscripts are first introduced as a part of the standard formula for slope, subscripting may be confusing. The model presents a related and important idea and another example of how subscripting is used. Subscripts are clarified as distance is illustrated. In precalc when the distance on a plane is formally considered, many students consider distance as solely a two-space concept. The model encourages, "reminds," or "reintroduces" distance in one-dimension and sets the stage for a calc II topic of distance in three-space. Introducing it in precalc/algebra II permits generalization and permits a student to see the bigger picture. Is the heuristic argument route the only ways to effectively present the topic? Does this reviewer believe all students think better following a verbal argument rather than examining something with their hands? Has the reviewer ever relinquished control of center stage and experimented with silence and a model instead of "chalk and talk?" Did the reviewer cut out the model and use it in his or her classroom before deciding the article was "not suitable for publication?" Are models and manipulatives only suitable for those who can not follow "a Polya-like" discourse? Might Polya have introduced such a model into his classroom? Reviewer 2:"The use of a box is the obvious model for this situation. Any available box, e.g. a shoe box, will work as well." Author's Response:Absolutely, "a box is the obvious model for this situation." Wasn't a box used? Did the reviewer's "any available box" provide a true model for the distance or did the reviewer also condone the use of a stick or string or printed line segment to serve that purpose? Does the reviewer suggest pointing from corner to corner and announcing the coordinates and the distances and their symbols? Has the reviewer ever used this strategy? What happened to the student who was a little bit slow in the uptake and concentrating on the prof's previous words but losing the prof's new sentence? Did the "any box" provide a permanent record of what the handler called the important lengths? If the reviewer suggests a plain unprinted box as the ideal tool for having the student label the sides, then the suggestion should have been made as a suggestion not as a reason for nonpublication. Reviewer 3:"Doesn't pre-printing everything on the model give the students exactly what we want them to figure out for themselves?" Author's Reply:The author doesn't want students to "figure everything out for themselves." Perhaps this point of view is more valuable for the reviewer. The sides are labeled symbolically so that student can mentally verify their correctness and see the bigger picture. Correctly coding is secondary to concretely representing distance in one- two- and three-dimensions. If a prof doesn't wish to include labels, let the prof white them out and refocus the presentation to his/her own end. The author's stated goals were:
Are these inappropriate goals for an article? The author asks the reviewers the following questions.
|
|
‘Relinquishing Control of Center Stage'
The author passionately proposes the reader, and most certainly anyone reviewing the material presented, change the format of the class from teacher-center exposition to student-controlled experimentation and discovery before making a value judgement about concrete thought and the use of this or any other manipulative. Concrete thought does not happen abstractly unless one is experienced in concrete thought. The professor or reviewer who chooses not to take model in hand HAS NOT EXPERIENCED CONCRETE THOUGHT. The professor or reviewer who has not taken model in hand has perhaps REPRESSED this language. See www.mathnstuff.com/papers/langu/page2.htm. |
|
Students Who Have No Difficulty With This Topic
One reviewer negated the value of the manipulative claiming "students have no difficulty with this topic." Who is to say that student would not gain more using the manipulative. Who is to say the student who appears to "get it" and memorizes a formula would not, with the manipulative, understand better the origin of the formula. Who is to say the student who doesn't make it to calc II where three-space distance is addressed, would not easily in algebra I or algebra II really "get it" through the concrete manipulative. |
|
Your Goals If for you "chalk and talk" is not the only way to communicate mathematics and if the goals stated by the author and the AMATYC Standards match your own, experiment with the distance manipulatives and the debriefing contained herein. |
| 1 Fred R. Barnard, as recognized by William Safire in William, ‘Worth A Thousand Words," The New York Times Magazine, April 7, 1996, pg. 6 - 16. |

|