Ernest Ranucci's Tetra-tetra Flexagon

Once Upon A Time, in the 1970s at an NCTM meeting, I sat in a room with a hundred other math teachers and folded my first tetra-tetra flexagon.   Ernest Ranucci guided us through the paper-folding process and each of us (I think) experienced the joy of making something so beautiful and simple. The wonder of that moment and the cut and folded flexagon came home with me. The directions for its assembly did not.   I experimented for quite some time before my new flexagon did what I wanted it to do.   So, I take blame for the graphics and the directions but not for the idea.

There are two versions of this page. The ORIGINAL VERSION has step-by-step written instructions. This ONE IMAGE VERSION has a large image and a list of all pages and the animation below.

"Ernest Ranucci's Tetra-tetra Flexagon" - ORIGINAL 9/23/98 VERSION Take a sheet of paper, fold it, and the fun begins. Directions for folding and the front and back of an illustrated tetra-tetra flexagon. STEP-BY-STEP INSTRUCTIONS "Ernest Ranucci's Tetra-tetra Flexagon" - 11/2025 VERSION Take a sheet of paper, fold it, and the fun begins. Directions for folding and the front and back of an illustrated tetra-tetra flexagon. ONE IMAGE W/INSTRUCTIONS & EACH PAGE LISTED

• 1 piece of "Scotch" tape about 6 cm long
• scissors
• ruler
• a piece of paper (possibly illustrated on the front and back with the pictures provided)

Printed Tetra-tetra Flexagon

The two gif images printed below should be center and duplicated on the front and back of an 8 1/2" by 11" sheet of paper. The image size is 8" by 10".

The user is reminded that the author/artist gives permission for the material and graphics to be duplicated as is for nonprofit purposes.

For larger, more useful copies of these graphics, place your mouse on the graphic, right click, save the picture as a file with a name of your choice.

Click on image to see just image.

How to Flex a Tetratetra Flexagon

"Bend the book back on its binding."

1st: Hold the panels as one would hold an open book: hold the right and left edges with the right and left hands.

2nd: Work the creases so the "book" opens and closes easily.

3rd: Bend the "book" back pushing the binding up (breaking the binding). If the flexagon does not separate at the crease between the adjacent panels, assist the separation with your thumbs. If this is still not possible, turn the flexagon over so the back of the panels is visible rather than the front, and try bending it back again.   Either the back or the front will flex to reveal new panels.

These Graphics

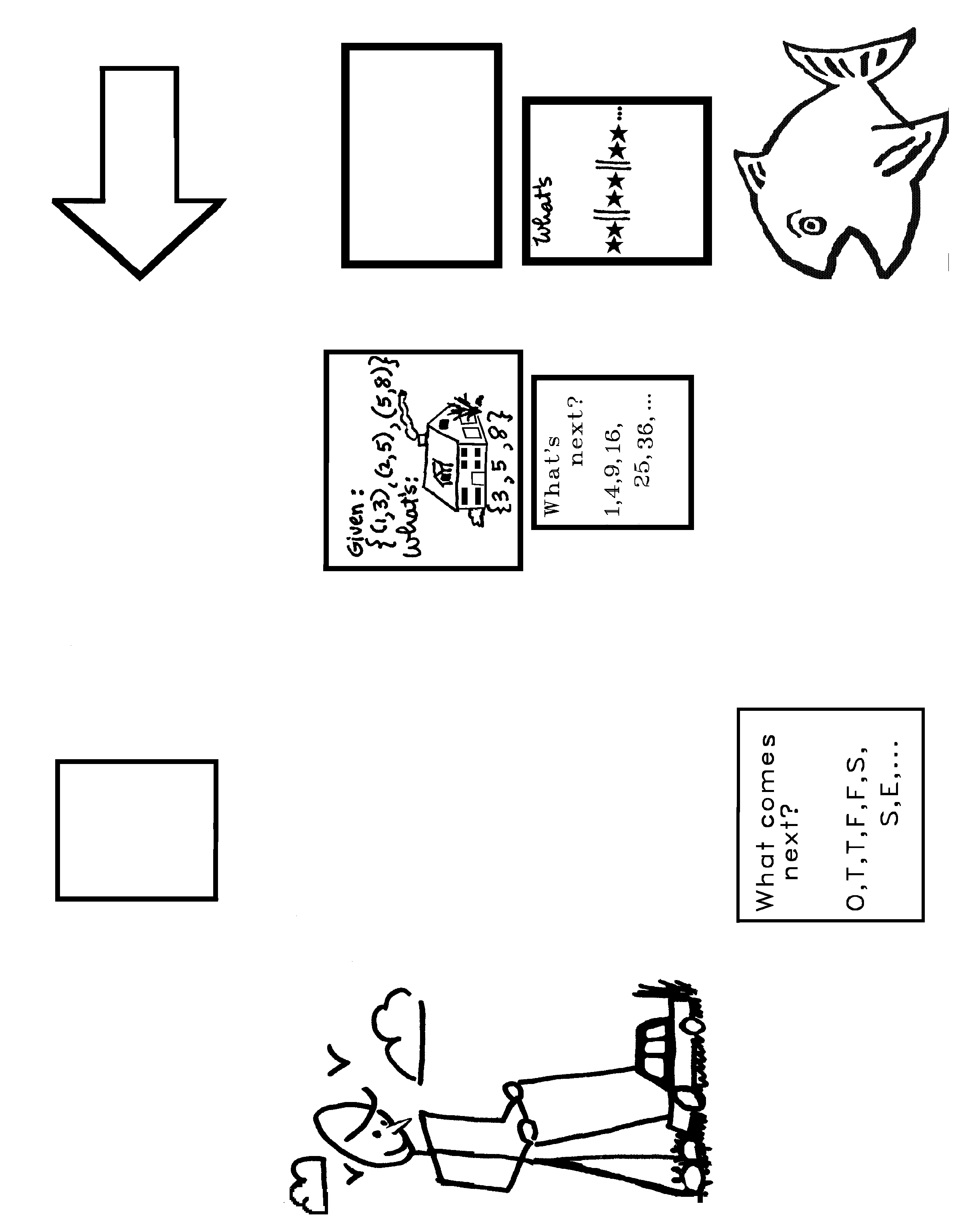
Before using the flexagon illustrated in the following pages, it is important to know the answers to the questions it poses. The house drawn above the set containing the numbers 3, 5, and 8 is a "Home on the Range." The next number in the sequence 1, 4, 9, ..., is the next square, 49. The next letter in the sequence, 0, T, T, F, F, S, S, E, ... is N, for nine (one, two , three, etc.).

The figure in the box represents "Stars and Stripes Forever." The empty rectangles are drawn so the user may draw his/her own figures or questions or riddles. Math daffinitions are a lovely idea also. For example, the figures below might be considered "scrambled eggs" and "rectangles [wrecked angles]."

The blank spaces on the flexagon's panels are left so one can draw or write their own commutative or noncommutative figures or words.   Words like "cake" and "pan" noncommutatively switch to "pan cake."

Panel A has: "Questions:"

Panel B has: "Answers:," clouds, flowers, the logos.

Panel C has: arrow, "subtraction," baby fish.

Panel D has: "Don't argue" and "exponents."

The back of panel A has: clouds and lawn mower.

The back of panel B has: empty box, etc.

The back of panel C has: "home on the range," etc.

The back of panel D has: arrow, empty boxes, momma/monster fish.

from Flexagons and Kaleidocycles, © 1997, Agnes Azzolino, ISBN 0-9623593-8-6 mathnstuff/papers/tetra/tetra.htm © 9/23/98, 5/2017, 6/23/2022, 11/10/2025, A2, Agnes Azzolino