MIDDLE GROUND - Answers

 

 

 

Normal Distribution   1. Complete: The mode of a normal distributions is the mean, the median.   2. Complete: 50 percent of a scores in a normal distribution are above the mean.   3. In the figure above, the symbols p(-2 < x < 2) is read, "the probability a standard normal score is between -2 and 2," or, "the probability a standard normal score is within 2 standard deviations of the mean." State this probability as a number. 95% or .952   4. For a standard normal distribution, state: a. p(z > 0) = 50% b. p(z < 0) = 50% c. p(z = 0) is 0. It is not an area. If answer a. and answer b. add up to 100% or 1, answer c. must be zero. d. p(z > 2) = 2.2% + .2% = or .024 or 2.4% e. 1 - p(z > 2) = 1 - .024 or 97.6% f. p(z < 2) =1 - p(z > 2) = .976 or 97.6% g. p(-3 < z < 3) = 99.6% or .996 h. p(-2 < z < -1) = 13.6% or .136 i. p(z < -1) = .16 or 16%   5. A normal distribution has a mean of 10 and a standard deviation of 2. What's the probability a. a score is within 1 standard deviation of the mean? 68% or .68 b. a score is between 10 and 12? 34% or .34

 

 

Standard Normal   1. Complete: The mean of the standard normal distributions is 0.   2. Complete: The standard deviation of the standard normal distributions is 1.   3. Given a normal distribution with a mean of 75.4 and a standard deviation of 12.32, a. estimate p(50 < x < 88), about 82%     b. p(x > 63) 83.8%     c. p(x < 100) 97.8% or .978   4. State the z-score which matches a score of 12.6 from a normal distribution given the mean is 10 1/2 and the standard deviation is 1.25. It is (12.6 - 10.5)/1.25 is 1.82608.   5. State the probability a score is greater than 25 if the distribution is normal, the mean is 20, and the standard deviation is 5.   Show pencil & paper work.     6. Terry and Tony each got an 88 on stat tests but they were different but equivalent tests. The teachers were willing to state the mean and standard deviation for each test. Below are the statistics. Who got the better grade? Terry Tony grade: 88     grade: 88 : 74 : 78 s: 11.2 s: 9.2 z: 1.25, higher grade z: 1.087

 

 

Stanine   1. Explain the word stanine. Standard nine intervals centered about the mean with the 5th or center interval being within 1/4 standard deviation of the mean and each of the other intervals also being 1/2 standard deviation in width.   2. Given the standard normal distribution, compute the probabilites. a. p(-1.75 < z < -.25) is 7% + 12% + 17% = 36% or .36     b. p(z is not in the interval -1.75 < z < -.25) = 1 - .36 = .64   c. p(z < -1.25) = 4% + 11% = 15% or .15   3. Given a normal distribution with a mean of 65 and a standard deviation of 10, a. estimate p(52.5 < x < 62.5) x of 52.5 is z of -1.25, x of 62.5 is z of -.25, 12% + 17% = 29% or .29   b. 1 - p(x < 72.5) = 100% - ( 4% + 7& + 12% + 17% + (20%) + 17%) = 100% - 77% = 23% or .23   c. p(x > 72.5) = 1 - .77 = .23 or 23%, since x of 72.5 is z of .75   4. Each year students are tested and parents wish to understand the scores. This year's math grades were normally distributed with a mean of 65 and a standard deviation of 10. Use stanines to explain to the parents how well their chidren did if the scores for 4 children were 98, 23, 66, and 80.

x	z	stanine	Explanation
9.8	3.3	9	in the top 4% of all scores, better than 96% of all scores
23	- 4.2	1	very, very poor
66	.1	5	average, better than half of all scores
80	1.5	8	superior performance, in the top 11% of all scores, better than 89% of all scores

 

 

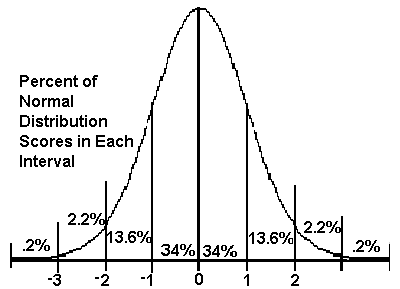
Questions with Answer Page   1. State the area under the standard normal curve between z-scores of 0 and 1.42.     42.22% or .4222   2. Given the standard normal distribution, compute p(z is within 1.42 standard deviations of the mean), p(-1.42 < z < 1.42).     84.44% or .8444   3. Given the standard normal distribution, find the z-score such that p(z is within __ standard deviations of the mean) = 95%. Half of 95% is 47.50%, and matches a z-score of 1.96, the answer.   4. Find, to two decimal places accuracy, the boundaries in the standard normal distribution, such that p(z is within __ standard deviations of the mean) = 74.98%. Half of 74.98% is 37.49%, and matches a z-score of 1.15, the answer.   5. Using the z-scores in the above table, state the lowest z-score which is in the top 90% of all scores. The z-score required matches an area of 40%, 90% - 50%. The lowest z-score is 1.29, matching an area of 40.15%.   6. Using the z-scores in the above table, state the lowest z-score which is in the top 85% of all scores. The z-score required matches an area of 35%, 85% - 50%. The lowest z-score is 1.04, matching an area of 35.08%.   7. Compute: p(-2.2 < z < -2.35). answer is .45%, work is at   8. Compute, given a normal distribution, = 3 and s = 0.4, p(2 < x < 4). answer is 98.76%, work at

 

 

© 2005, Agnes Azzolino www.mathnstuff.com/math/spoken/here/2class/90/ans90.htm