


 |
 |
|
This page contains a more detailed examination of the behavior of the sine (vertical component of the angle or ratio of opposite leg to hypotenuse) and cosine (horizontal component of the angle or ratio of adjacent leg to hypotenuse) functions. For a broader view on trig functions see the Unit Circle Page. |
 |
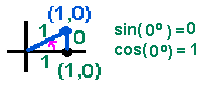 Once you get past the fact that you are working with a triangle having an angle of 0° and a side with length 0, it's easy. |
| The vertical leg is 0, so the sine is 0. The horizontal leg is the same as the radius, which is 1. So, the cosine is 1. Next consider another way of saying exactly the same thing, but by describing the angle itself and the unit circle, not just the triangle. There is no vertical component of the angle: The vertical component of the angle is 0, so, the sine of 0° is 0. The horizontal component of the angle is as large as it can get. The radius is 1, so the horizontal component is 1: The cosine of 0° is 1. | |
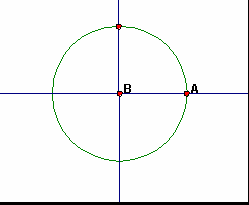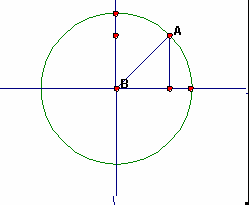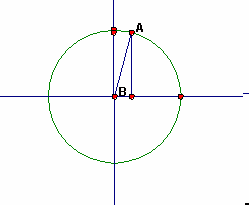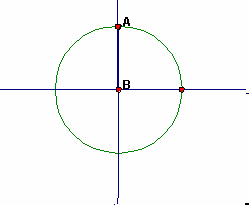 |
As the angle increases from 0° to 90°, the sine increases from 0 to 1. As the angle increases from 0° to 90°, the cosine decreases from 1 to 0. |
 /2 Radians
/2 Radians
 |
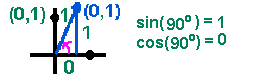
Again you have an angle of 0° and a side with length 0. This time the vertical leg is 1, the same as the radius, so the sine is 1. |
|
The horizontal leg is 0, since there is no horizontal component of the triangle, so, the cosine is 0. Consider the angle itself and the unit circle. There is no horizontal component of the angle: The horizontal component of the angle is 0, so, the cosine of 90° is 0. The vertical component of the angle is as large as it can get. The radius is 1, so the vertical component is 1: The sine of 90° is 1. | |
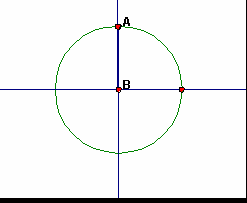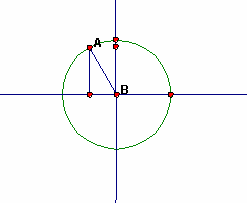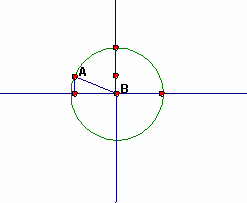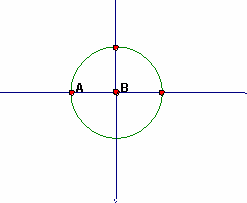 |
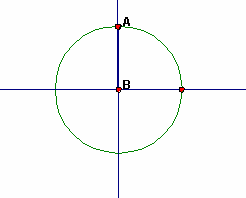
As the angle increases from 90° to 180°, the sine decreases from its maximum value of 1 to a value of 0. As the angle increases from 90° to 180°, the cosine increases in magnitude, but is now a negative value. The cosine goes from 0 to -1. |
 Radians
Radians
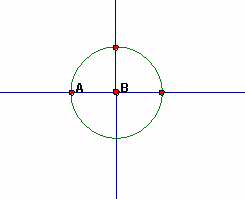 |
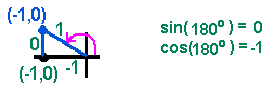 Again you have an angle of 0° and a side with length 0. Values are stated above. Again consider the central angle itself and the unit circle. There is no vertical component of the angle: The vertical component of the angle is 0, so, the sine of 180° is 0. The horizontal component of the angle is as large as it can get, but, it's also negative. The horizontal component is -1: The cosine of 180° is -1. |
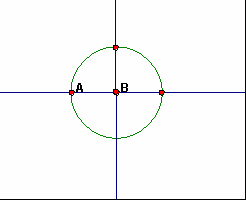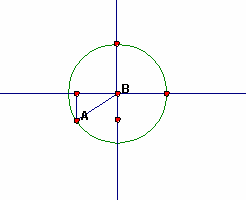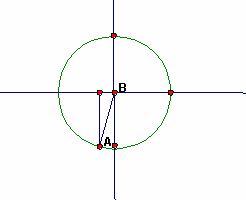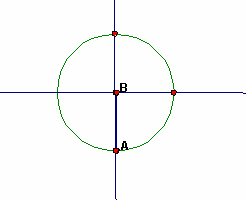 |
Both x and y coordinates are negative in the third quadrant. Since the hypotenuse is a +1, both the sine and the cosine must be negative. |
|
As the angle increases from 180° to 270°, the sine increases in magnitude but is now negative, so, the sine decreases from 0 to -1. As the angle increases from 180° to 270°, the cosine decreases in magnitude but is now negative, so, the cosine increases from its minimum of -1 to a value of 0. | |
 /2 Radians
/2 Radians
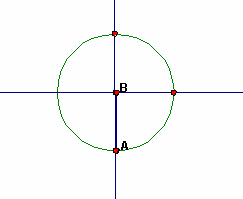 |
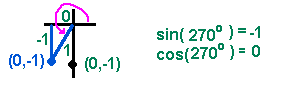
Again you have an angle of 0° and a side with length 0. Values are stated above. Consider the central angle itself and the unit circle. There is no horizontal component of the angle: The horizontal component of the angle is 0, so, the cosine of 270° is 0. The vertical component of the angle is as large as the radius, but it's also negative. The vertical component is -1: The sine of 270° is -1. |
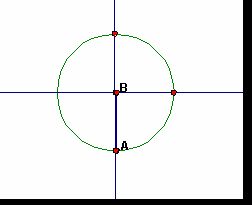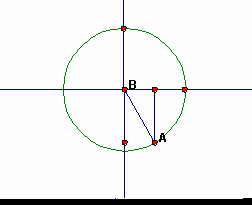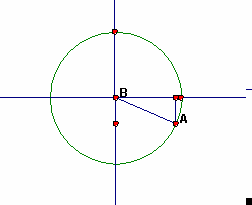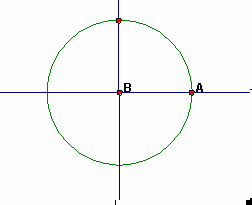 |
As the angle increases from 270° to 360°, the sine increases from -1 to 0. As the angle increases from 270° to 360°, the cosine increases from 0 to +1. |
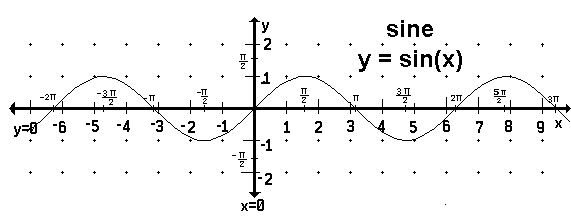

 | ![[MC,i. Home]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
![[Table]](http://www.mathnstuff.com/math/spoken/here/1gif/table.gif)
![[Words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)

![[this semester's schedule w/links]](http://www.mathnstuff.com/gif/semestr.gif)
![[Good Stuff -- free & valuable resources]](http://www.mathnstuff.com/gif/goods.gif)
![[next]](http://www.mathnstuff.com/math/spoken/here/1gif/next.gif)
![[last]](http://www.mathnstuff.com/math/spoken/here/1gif/last.gif)
© 2006, Agnes Azzolino www.mathnstuff.com/math/spoken/here/2class/330/unitsin.htm |