Intro
This page was envisioned to give the reader exposure and play time with many functions,
their slope functions (derivatives), and their area functions (integrals), prior to a discussion on the uniqueness
of the exponential function, ex.
In each colored computation box, enter the required info, press/click the gray button, see the resultant computation.
Enter negatives as "-x" rather than "- x" on this page. Do NOT write input x values as fractions.
Write fractions as good decimal approximations. CLICK ON THE GRAPH TO SEE AN ENLARGEMENT.
Sometimes questions are written above or below a box. If possible, answer the question then, with the mouse, swipe the page
between the two stars to see the answer to the question.
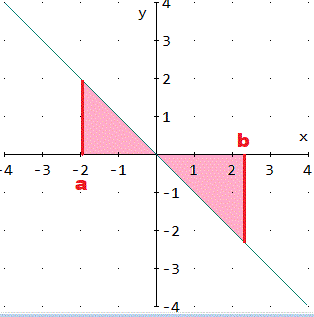
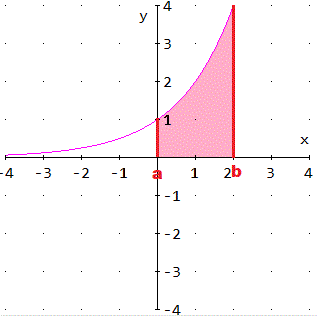
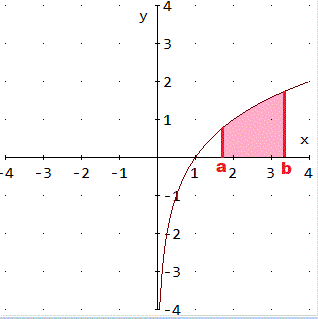
To find the "area under a curve," from the point (a,0), draw a perpendicular to the
point (a, f(a)) on the curve. One may need to draw it "up" to the curve or "down" to the curve. Repeat this procedure for b.
Shade the area between x=a and x=b which is between the curve and the x-axis. This is the area needed. If instead the area between
two curves (say f(x) and g(x)), from a to b, is needed, draw the perpendiculars x=a and x=b. Shade the area between the curves.
The computation is covered on the derivative page listed below.
An area may be negative. An area is negative if the curve falls below the x-axis.
See the second example under "Arithmetic Tricks, Rules & Shortcuts In Words & Symbols" on page
Derivatives and Integration.
For other information, go to the pages listed below.
For additional information on the function of this page and other functions see
Function and Relation Library. For additional information on trig functions see
Trig Functions Library.
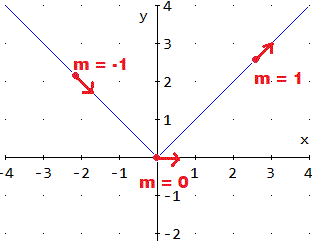
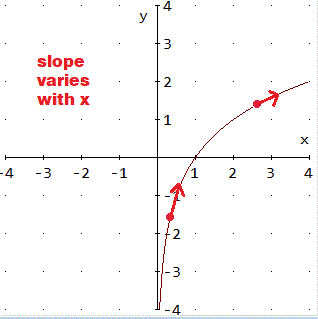
Enjoy. |  x, or x1/2
x, or x1/2
 1,
1, 

 1,
1, 


























![[master list of all MSH! dictionary words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)

![[Good Stuff -- free & valuable resources]](http://www.mathnstuff.com/gif/goods.gif)

![[MC,i. Home, site home page]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)


