end behavior

IN MATH: 1. n. A function's values for extreme values of its variable; the value a function, f(x) approaches when x is extremely large or when x is extremely small; the function value, f(x) or y, approximated by the value of another function defined by the curve which is approached but never "reached" by a graph.

asymptote

IN ENGLISH: 1. as defined above.

	EX. 1: When x is extremely large, the values of f(x) are close to the values of y = 0, so, f(x) is positive and approximately 0. When x is extremely small, the values of f(x) are close to the values of y = 0, so, f(x) negative and approximately 0.
	EX. 2: When x is extremely large, the values of f(x) are close to the values of y = 4, so, f(x) is approximately 4. When x is extremely small, the values of f(x) are close to the values of y = 4, so, f(x) negative and approximately 4.
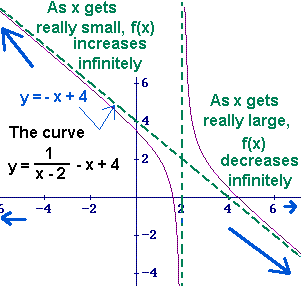
	EX. 3: When x is extremely large, the values of f(x) are close to the values of y = -x + 4, which is increasing infinitely, so, f(x) is increasing to positive infinitely. When x is extremely small, the values of f(x) are close to the values of y = -x + 4, which is decreasing infinitely, so, f(x) is decreasing to negaive infinity.
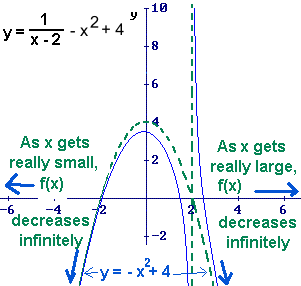
	EX. 4: When x is extremely large, the values of f(x) are close to the values of y = - x² + 4, which is increasing infinitely, so, f(x) is decreasing to negaive infinitely. When x is extremely small, the values of f(x) are close to the values of y = - x² + 4, which is decreasing infinitely, so, f(x) is decreasing to negaive infinity.

APPLICATION: See list 230.

This is a page from the dictionary MATH SPOKEN HERE!, published in 1995 by MATHEMATICAL CONCEPTS, inc., ISBN: 0-9623593-5-1. You are hereby granted permission to make ONE printed copy of this page and its picture(s) for your PERSONAL and not-for-profit use.

$[MC,i. Home]$ $[Table]$ $[Words]$ $Classes$

[Good Stuff -- free & valuable resources]

$[next]$ $[last]$