
IN MATH: 1. n. a denomimator (divisor, bottom number) shared by two or more fractions. EX.
Common denominators are needed to add fractions.
A common demonimator is not just the product of the factors the fractions have in common but,
THE FACTORS THEY HAVE IN COMMOM AND THE FACTORS THAT MAKE EACH FRACTION DIFFERENT.
A common demonimator includes all factors from each fraction and there are many common denominators.
The LEAST COMMON DENOMINATOR is the smallest product of the factors of each fractions .
Here are two methods for FINDING THE LEAST COMMON DENOMINATOR, the smallest product of the
factors of each fractions .
Common Factors First Method. - Factor each demonimator -- usually factor as a
prime factorization.
- List the common factors, the factors each fraction shares, writing that factor only once.
- Add to the list the factors each fraction does not share, listing only once the ones they have
in common with some of the other fractions.
- The list of factors is the common denominator. Multiply the factors together if needed.
One Fraction At-A-Time Method.
- Factor each demonimator -- usually factor as a
prime factorization.
- List each factor of the first fraction.
- Add to the list the factors of the second fraction which have not already been listed.
- Repeat step 3 for each fraction.
- The list of factors is the common denominator. Multiply the factors together if needed.
In the examples below, the lines starting at the top of the example show the
first step in the work.
Ex. 1. Find the common denominator for 5/12 and 3/4.
Common Factors First
The common factors are 2 and 2. The first denominator also has a 3. The common denominator
is 2·2·3 or 12.
| 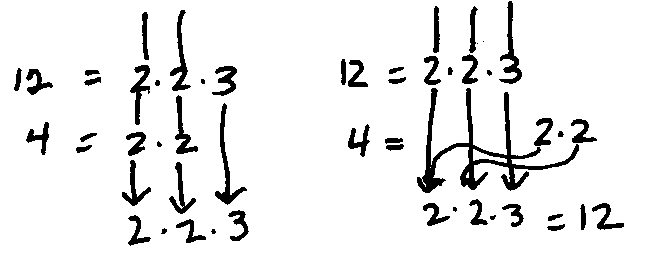 |
One Fraction At-A-Time
The first denominator has factors of 2 and 2 and 3.
The second denominator has factors of 2 and 2 and these are already listed. No new factors need be listed.
|
Ex. 2. Find the common denominator for 2/3 and 3/4.
Common Factors First
There are no common factors.
List each fraction's factors. The common denominator is 2·2·3 or 12.
| 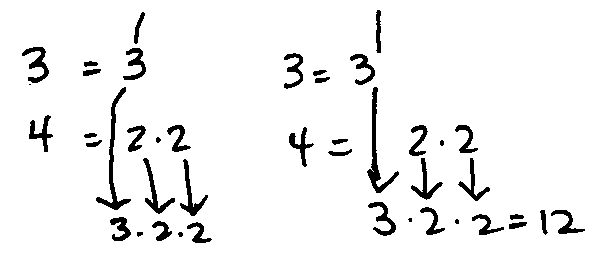 |
One Fraction At-A-Time
The only prime factor of 3 is 3. Next, list the factors of 4.
The common denominator is 2·2·3 or 12.
|
Ex. 3. Find the common denominator for 1/6, 1/2, 5/12, 2/15.
Common Factors First
There is no common factor of 6, 2, 12, and 15. Next most common is 2 and 3, so list these avoiding
duplication. An additional 2 and an additional 5 are required.
The common denominator is 2·2·3·5 or 60.
|  |
One Fraction At-A-Time
The prime factors of 6 are 2 and 3, so, list each. The prime factor of 2 is 2 but, it has already been
listed. The prime factors of 12 are 2 and 2 and 3. The 2 and 3 are duplicates, so, just list one more 2. The
prime factors of 15 are 3 and 5. List the 5, but, don't duplicate the 3 which is already listed.
The common denominator is 2·2·3·5 or 60.
|
Ex. 4. Find the common denominator for 3/10 and 4/25.
Common Factors First
Ten and 25 share a common factor of 5, so, list it. The additional factors of 2 and 5 are required.
The common denominator is 2·5·5 or 50.
|  | One Fraction At-A-Time
List the factors 2 and 5 for the denominator 10. Don't list the duplicate factor of 5, but, do list an
additional factor of 5 for the factors of 25. The common denominator is 2·5·5 or 50. |
Example 5 is very much like example 4. One has arithmetic factors, the other algebraic factors.
The procudure is the same.
Ex. 5. Find the common denominator for 2/x2 and -3/(xy).
Common Factors First
Each denominator has a factor of x. List it only once. Next list the two required factors of x and y.
The common denominator is x·x·y or x2y.
| 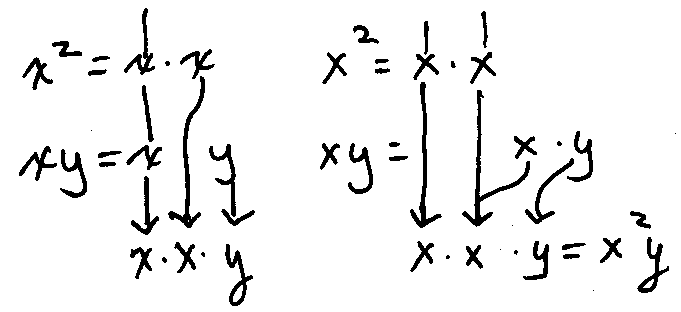 | One Fraction At-A-Time
The first fraction has denominator factors of x and x. List each. The next fraction has factors of x and y.
Do not duplicate the x. List the y. The common denominator is x·x·y or x2y.
|
Ex. 6. Find the common denominator for 2x/(4x+4y) and -3/(2x-2y).
Common Factors First
The
binomials 4x+4y and 2x-2y have only 2 as a
common factor. List it. Other unique factors needed are x+y, x-y, and 2. List each. The common denominator
is 2·2·(x+y)·(x-y) or 4x2-4y2.
|  |
One Fraction At-A-Time
The first fraction has a denominator prime factors
2, 2, and x+y. List these. The second denominator has a duplicate factor of 2 and a unique factor of x-y. List
only the x-y. The common denominator is is 2·2·(x+y)·(x-y) or 4x2-4y2.
|
Ex. 7. Find the common denominator for 5/(x2-1) and 3/(x2+4x+3).
Common Factors First
The fractions have a common denominator factor of x+1. List it. They have unique factors of x-1 and x+3.
List them. The common denominator is (x+1)(x-1)(x+3).
|  |
One Fraction At-A-Time
The first fraction as denominator factors of x+1 and x-1. List them. In the second fraction's denominator
the x+1 is a duplicate. Don't list it. The x+3 is needed. List it. The common denominator is (x+1)(x-1)(x+3).
|
Ex. 8. Find the common denominator for 5/(2x + 8) and 4/(x2-16).
Common Factors First
The denominators have a common factor of x+4. List it. Unique factors of 2 and x-4 are also needed.
List them. The common denominator is 2(x+4)(x-4).
|  |
One Fraction At-A-Time
The first fraction has denominator factors of 2 and x+4. List them. The second fraction has a
duplicate factor of x+4. Don't list it. It has a unique factor of x-4. List it. The common denominator is 2(x+4)(x-4).
|
Ex. 9. Find the common denominator for 4/(9ab2) and (a+1)/(12a2b3) .
Common Factors First
The common factors are 3, a, b, and b. List them. There are unique factors of 2, 2, a, 3, and b. List these also.
The common denominator is 2·2·3·3·a·a·b·b·b or 36a2b3.
| 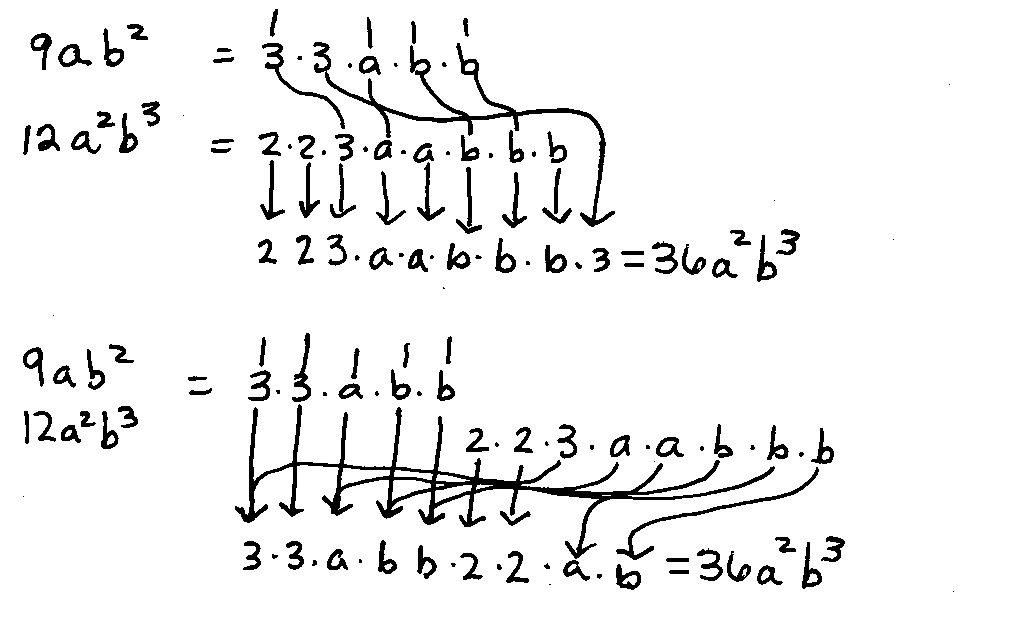 | One Fraction At-A-Time
The first denominator has factors of 3, 3, a, b, and b. List them. The next fraction has duplicate
factors of 3, a, b, and b. Do not list these. List the unique factors of 2, 2, and b. The common denominator
is 2·2·3·3·a·a·b·b·b or 36a2b3.
|
IN ENGLISH: 1. n. a characteristic shared by two or more things or people. EX. Their common denominator was their love for mathematics.
APPLICATION: See list
40.
- Find the common denominator for:
- 1. 1/2 and 3/4
- 2. thirds and eighths
3. 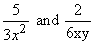 4.
4. 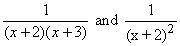


This is a page from the dictionary
MATH SPOKEN HERE!, published in 1995 by MATHEMATICAL CONCEPTS, inc.,
ISBN: 0-9623593-5-1. You are hereby granted permission to make ONE printed copy of
this page and its picture(s) for your PERSONAL and not-for-profit use.

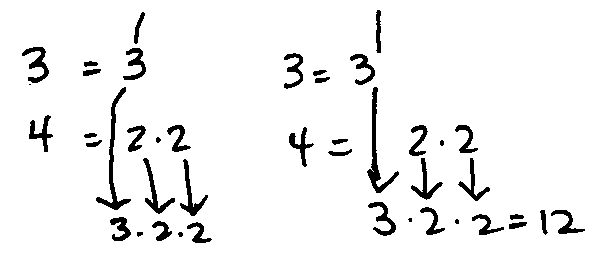


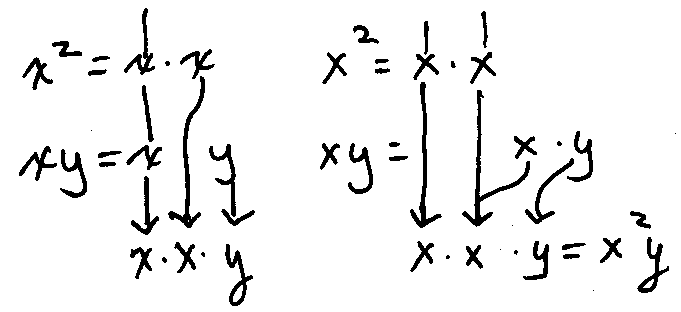



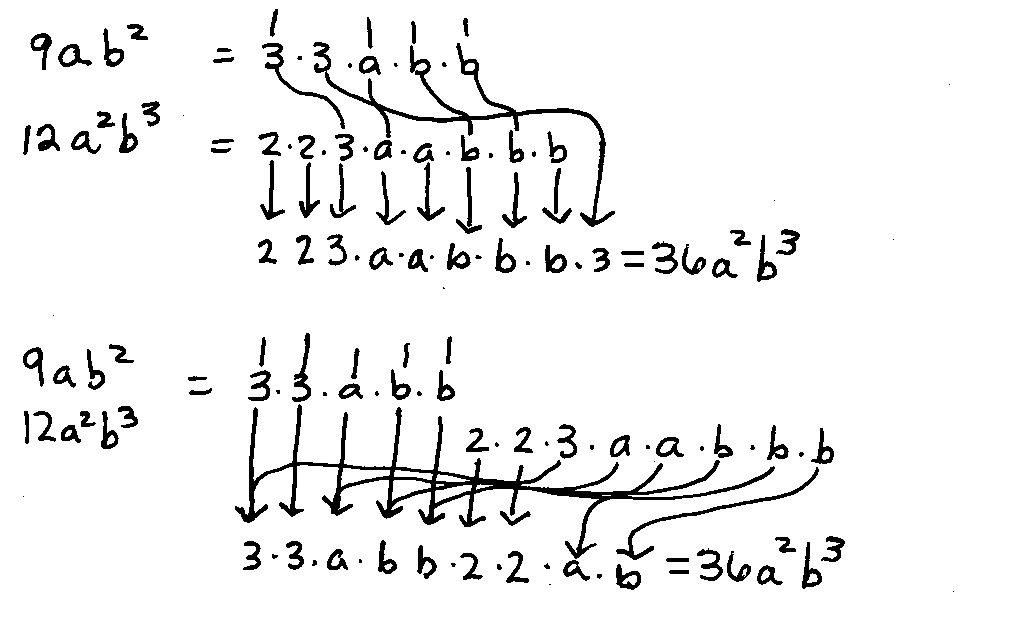

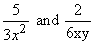
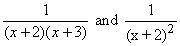


![[MC,i. Home]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
![[Table]](http://www.mathnstuff.com/math/spoken/here/1gif/table.gif)
![[Words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)

![[this semester's schedule w/links]](http://www.mathnstuff.com/gif/semestr.gif)
![[Good Stuff -- free & valuable resources]](http://www.mathnstuff.com/gif/goods.gif)
![[next]](http://www.mathnstuff.com/math/spoken/here/1gif/next.gif)
![[last]](http://www.mathnstuff.com/math/spoken/here/1gif/last.gif)