TermTiles&Tokens -- Manipulatives for Algebra

The Visual / Auditory / Symbolic / Kinesthetic Approach to Algebra

Solve Equations and Inequalities.

To solve means to find all numbers that make a statement true. To solve means to undo each operation from lowest to highest to reveal the value of 1x. Many of the equations used here may be solved mentally, but, that's really not the main goal. Here the goals are:

to use Term Tiles to solve equations and inequalities.
to review order of operations and inverse operations.
to examine the written work that parallels the manipulation required to solve equations and inequalities.

The first few steps of solving any equation or any inequality are the same: Chose the arrangement of display areas. Represent each expression. Simplify each expression, if possible. More sophisticated statements then require more steps before a solution is found.

Here one operation, then two operations, then many operations, then inequalities are discussed. Quadratics are discussed later.

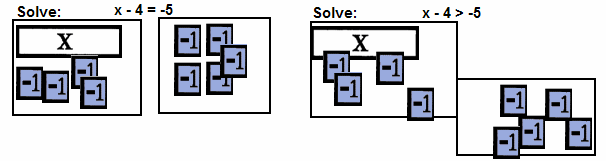
Choose the Display Area.

Equations require two display areas placed side-by-side at an equal distance from the student or edge of the desk. Solving an inequality requires two display areas with the "greater side" placed a greater distance from the student or the edge of the desk.

Simplify Each Side Before Beginning on Both Sides.

Work from left to right. First work on each expression separately. Works on the left side first, then work on the right-hand expression as much as possible.

Once each side of the statement is simplified, work may begin on both sides simultaneously. Each operation must be undone in the proper order. This is done by taking the inverse of each side.

We begin with equations having only one operation. Because most of these steps are not required to solve an equation involving one operation, just undo the operation.

Undoing One Operation --- What did they do to the x? How do you undo this?

The key questions to ask are: What did they do to the x? How do you undo this?

Solve A Linear Equation By Undoing One Operation.

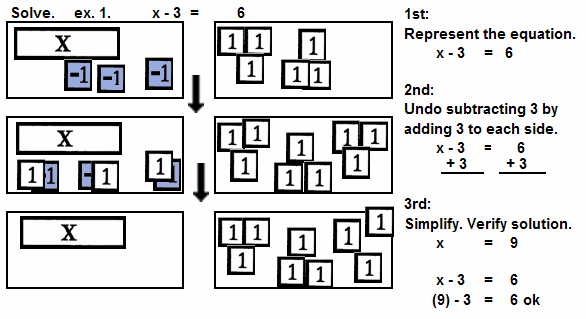
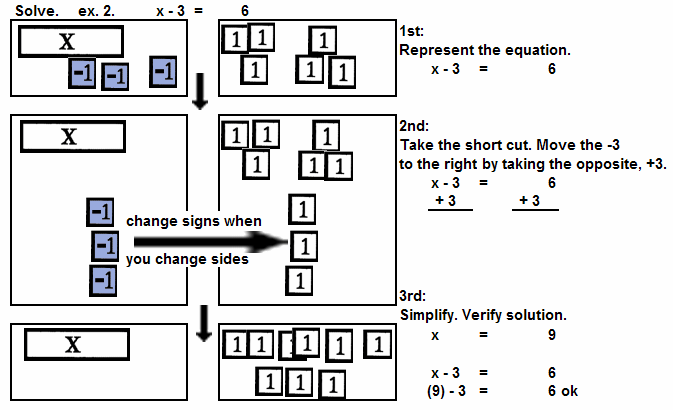
	x - 3 = 6	Undo subtraction with addition. See ex. 1 for use of inverse. See ex. 2 for use of "change the signs when you change the sides."
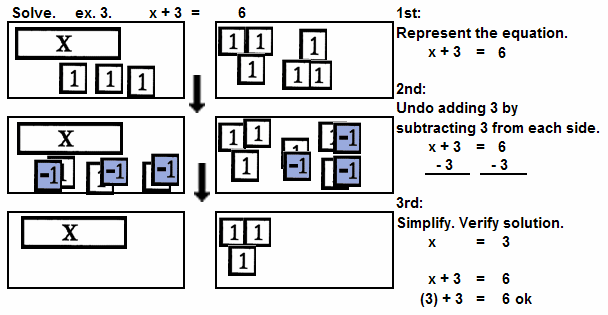
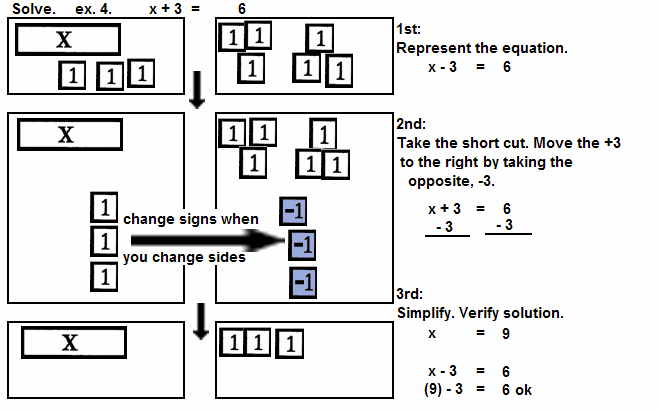
	x + 3 = 9	Undo addition with subtraction. See ex. 3 for use of inverse. See ex. 4 for use of "change the signs when you change the sides."
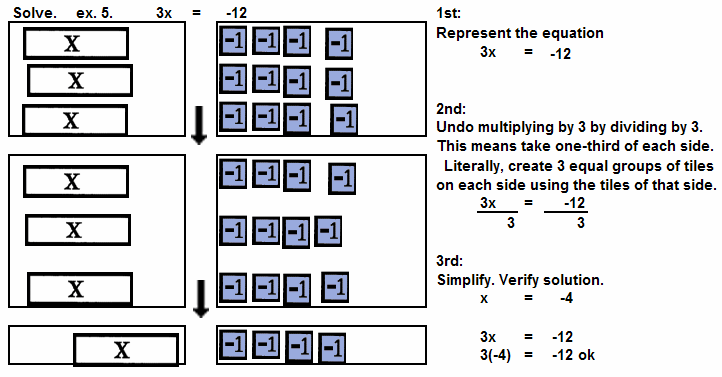
	3x = -12	Undo multiplication with division. See ex. 5.
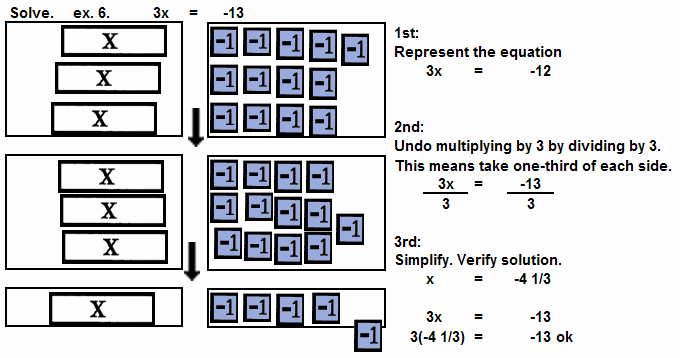
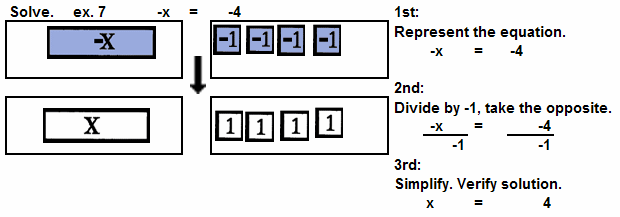
	3x = -13	Undo multiplication with division and have a remainder. See ex. 6.
	-x = -4	Undo multiplication by -1 with division by -1, taking the opposite. See ex. 7.
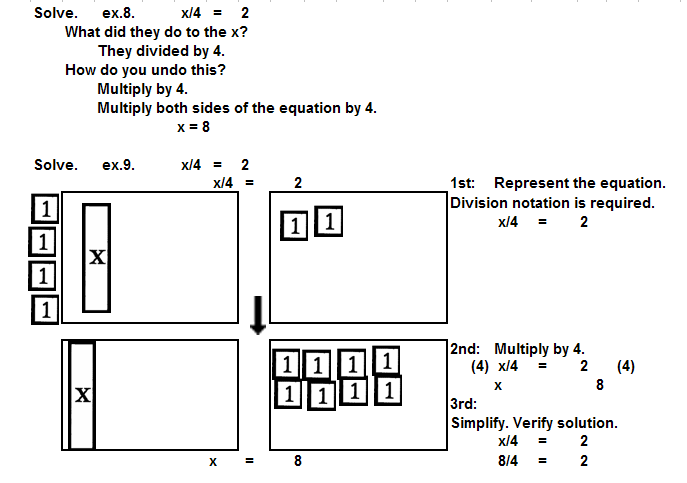
	x/4 = 2	Undo division with multiplication. See ex. 8. for MENTAL and VERBAL computation. See ex. 9. for manipulative computation.
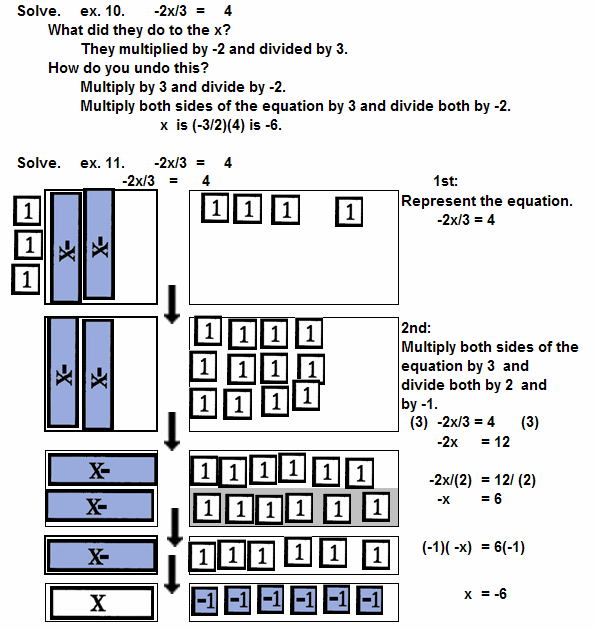
	-2x/3 = 4	Undo multiplication by a fraction with multiplication by its reciprocal. See ex. 10. for MENTAL and VERBAL computation. See ex. 11. for manipulative computation.