Consider the following examples.
|
 3 + 2x = 1 3 + 2x = 1
The two expressions "3 + 2x" and "1" do not mean the same thing but there may
be a time when they are equal. They are equal when -1 is used as the value of x.
The solution is -1. That is when the lines cross. That is when the expressions are equal.
3 + 2x = -1 The expressions "3 + 2x" is graphed. The
expression "-1" is not. Mentally graph "-1" and find all points where they are equal.
They are equal when -2 is used as the value of x. The solution is -2.
That is when this lines cross. That is when the expressions are equal.
|
|
 2x + 3 = 4x - 1 2x + 3 = 4x - 1
The two expressions "2x + 3" and "4x - 1" don't mean the same thing but there
may be a time when they are equal. They are equal, the lines cross, when x is 2, and only when x is 2.
The solution is 2.
|
|
 x + 2 = -x + 3 x + 2 = -x + 3
The two expressions "x + 2" and "-x+3" do not mean the same thing. There may
be a time when they are equal.
To solve x + 2 = -x + 3, find when they are equal. Find where the lines
cross. They cross only when x is 1/2. The solution is 1/2.
|
|
 x + 5 = 5 + x x + 5 = 5 + x
The two expressions "x + 5" and "5 + x" mean the same thing but are
said in different ways. They are always equal no matter what value of x is used in both expressions.
To solve x + 5 = 5 + x, find when they are equal, where the lines cross. They
cross for every value of x. They are always equal. The solution is all numbers.
|
|
 7 + x = x + 5 7 + x = x + 5
The two expressions "7 + x" and "x + 5" mean different things -- 7 more than
a number, 5 more than a number. They are never equal no matter what value of x is used in both expressions.
To solve 7 + x = x + 5, find when they are equal, where the lines cross. They
never cross for any value of x. There is no solution. |
|

















 ) =
) =
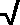 (2)/2, where -
(2)/2, where -
 <
<
 <
<


 ) =
) =
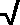 (2)/2, where 0 <
(2)/2, where 0 <
 < 2
< 2


 ) =
) =
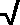 (2)/2
(2)/2 

 Solve
Solve 









 >
>

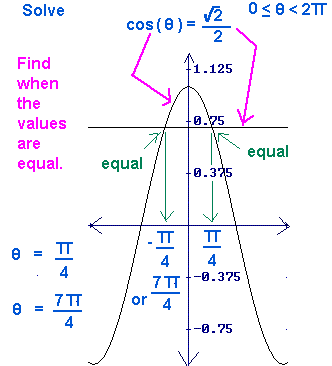





![[MC,i. Home, site home page]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
![[master list of all MSH! dictionary words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)

![[Good Stuff -- free & valuable resources]](http://www.mathnstuff.com/gif/goods.gif)
![[this semester's schedule w/links]](http://www.mathnstuff.com/gif/semestr.gif)