evaluate algebraic expressions

Intro & Vocabulary

      Usually, the instruction evaluate, simplify given all information, is introduced in algebra, and not used in arithmetic.

      One replaces the values of the variables with a constant or expression, then, simplifies the expression until a constant remains or like terms have been combined. [See Combine Like Terms.]

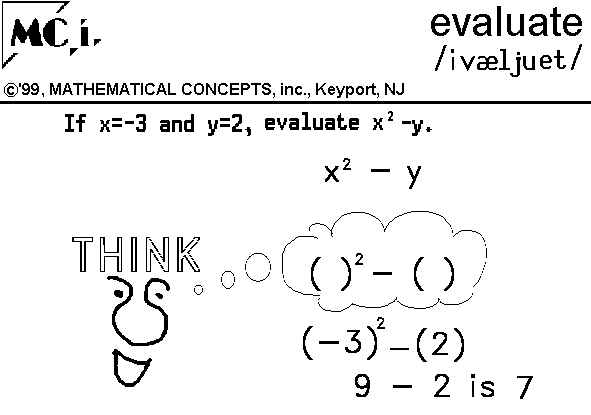
      When parentheses, (   ), are used, the task is simplified. The parentheses indicate the value of the variable is to be used. [Please read Writing One Operation Equations, Expressions, & Statements or just the use of "of" and check out the example given below which illustrates the meaning and use of parentheses.

 

Examples

 

1. Evaluate x² - 3xy + 2y when x= -1 and y = 2

 

1a.)     the meaning of parentheses               x2 - 3xy + 2y     (x)2 - 3(x)(y) + 2(y)   (-1)2 - 3(-1)(2) + 2(2)   +1 + 6 + 4     11, the answer

1b.) the way it usually looks               x2 - 3xy + 2y     (-1)2 - 3(-1)(2) + 2(2)     +1 + 6 + 4     11, the answer

1c.)     middle ground, writing each step out     x2 - 3xy + 2y   (  )2 - 3(  )(  ) + 2(  ) (-1)2 - 3(-1)(2) + 2(2)   +1 + 6 + 4     11, the answer

 

2. State f(2), f(-1), f(4) when f(x) = 2x + 4

2a.) x is 2     f(x) = 2x + 4           f(2) = 2(2) + 4     f(2) = 4 + 4     f(2) = 8

2b.) x is -1     f(x) = 2x + 4           f(-1) = 2(-1) + 4     f(-1) = -2 + 4     f(-1) = 2

2c.) x is 4     f(x) = 2x + 4           f(4) = 2(4) + 4     f(4) = 8 + 4     f(4) = 12

 

Exercises

Evaluate the expression when x = - 3 and y = 2.

3.)     x² - y

Answer x² - y (x)² - (y) (-3)² - (2) 9 - 2 7

 

4.)     4x - y

Answer 4x - y 4(x) - (y) 4(-3) - (2) -12 - 2 -14

 

5.)     4x - 3y

Answer 4x - 3y 4(x) - 3(y) 4(-3) - 3(2) -12 - 6 -18

 

6.)     xy - (x + y)

Answer xy - (x + y) (x)(y) - ((x) + (y)) (-3)(2) - ((-3) + (2)) -6 - (-1) -6 + 1 -5

 

 

7.) Evaluate 2x² + xy   when x is -1 and y = 4

Answers 2x² + xy 2(x)² + (x)(y) 2(-1)² + (-1)(4) 2 - 4 -2

 

Evaluate a Function  

8. Evaluate when f(x) = (x+1)² then MOUSEOVER the arrow to see the answer.

a.) f(3)

b.) f(-1)

c.) f(a)

d.) f(x - h)

 

 

Repeating the Process Prior to Point-Plotting

      In the above exercises, the same expression was used with different values of the variable. This procedure is required when generating points for point-plotting the graph of a function.

9. Complete the table of values and graph the line y = 4x + 2       x y 0     -1/2   2   -5/4   9. Complete the table of values and graph the line y = 4x + 2       evaluation showing work x y=4x+2 0 4(0)+2=0+2= 2 -1/2 4(-1/2)+2= -2 + 2= 0 2 4(2)+2=8+2= 10 -5/4 4(-5/4)+2= -5 + 2= -3 ordered pairs x y 0 2 -1/2 0 2 10 -5/4 -3 Complete the table. MOUSEOVER the arrow to see the answer . 10.) x y = -x/4 + 2 0   8   -4   -32                   11.) x y= 6 - 2x -1   3   2   0   © 6/28/05, A2, www.mathnstuff.com/math/algebra/qb/aevalu.htm