The Hexa-Flexagon

Assembly

1. Either a folded strip of 10 equilateral triangles [see next page] or a printed net of ten equilateral triangles is required. Accuracy is very desirable. Cut out the strip of triangles. Do not detach the triangles. Make a strip of 10 triangles adjacent to each other.
2. Lightly label the front and back of the strip as indicated. Each back triangle is numbered 10 greater than the same triangle on the front.
3. Score and fold each edge backwards and forwards so the creases are very flexible. Hold the strip as shown.
4. Fold triangles 1, 2, and 3 under triangles 4, 5, 6, 7, 8, 9, 10 as shown.
5. Fold triangles 7, 8, 9, 10 on top of triangle 6 as shown.
6. Place triangle 11 on top of triangle 19 rather than below it.
7. Lift triangle 20 and place it on top of triangle 11.
8. Curl a piece of tape around the right-hand edges of triangle 10 and triangle 11 beneath it.
9. The back of the flexagon should look like this.

How To Flex the Hexa-flexagon:

A. Use two hands to hold the flexagon in front of you.
B. Select two adjacent triangles which do not share a folded/creased edge. If you have selected correctly, you should be able to stick your finger into a "pocket" made by the overlapping triangles. But, you do not wish to do that. Pinch them together as directed in step C.
C. Pinch the two triangles together, common edge held tightest, PINCH WITH YOUR LEFT HAND.
D. Push the extension of the pinched common edge down and to the center of the flexagon. As in the figure on the night, pinch triangles 4 and 12 together while pushing the edge shared by triangles 17 and 18. PUSH WITH THE POINTER FINGER OF YOUR RIGHT HAND.
E. The flexagon will begin to open from the center as do the petals of a flower. Open the flexagon from the edge and bend the triangles back and outward from the center as you would the petals of a flower.

Trouble Shooting:

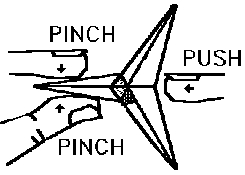
If a flexagon has not been folded accurately, it may need "help" flexing. This may be achieved by using a hole punch to remove the vertices of the triangles. This decrease the friction when flexing.

MATHEMATICAL CONCEPTS, inc.

85 First Street, Keyport, NJ 07735-1503, USA

732-739-3951

asquared@mathnstuff.com