
y=(x-2)2(x+4).
Who has this
with only a single root at x = 2?
 | I have y=(x-2)2(x+4). Who has this with only a single root at x = 2? |
 |
I have y=(x-2)(x+4). Who has a line with the same x-intercept as the axis of symmetry? |
 |
I have y=x+1. Who has the product of this and (x+5)3? |
 |
I have y=(x+1)(x+5)3 Who has this with the single root removed and a double root included when x=4? |
 |
I have y=(x-4)2(x+5)3. Who has this with only a double root when x=-5? |
 |
I have y=(x-4)2(x+5)2. Who has this concave up, with triple roots? |
 |
I have y=(x-4)3(x+5)3. Who has this reflected about y=0? |
 |
I have y=-(x-4)3(x+5)3. Who has this with single roots and concave up? |
 |
I have y=(x-4)(x+5). Who has this with the root at x=-5 removed, f(x) goes to - 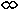 as x goes to - as x goes to -
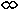 , , and a double root at x=2 added? |
 |
I have y=(x-2)2(x-4). Who has this reflected about y=0? |
 |
I have y=-(x-2)2(x-4). Who has this without the double root? |
 |
I have y=-(x-4). Who has the perpendicular to this at (-4,0)? |
 |
I have y=x+4. Who has this the x-intercept of this? |
|
I have (-4,0). Who has the the polynomial function with this root and a double root at x=-3? |
 |
I have y=(x+3)2(x+4). Who has the degree of this polynomial? |
| I have 3rd. Who has the end behavior of y=(x+3)2(x+4) as x increases without bound? |
| I have Who has the second degree polynomial with real roots of ± 2? |
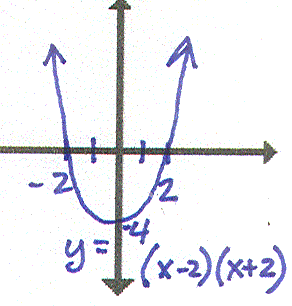 |
I have y=x2- 4. Who has the fourth degree polynomial with double roots of ± 2? |
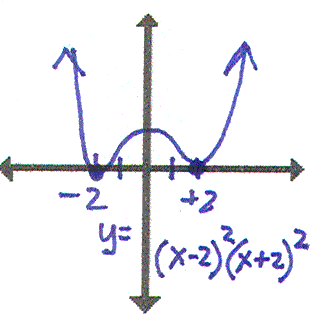 |
I have y=(x-2)2(x+2)2. Who has the fourth degree polynomial with a single root at x=2 and a triple root at x=-2? |
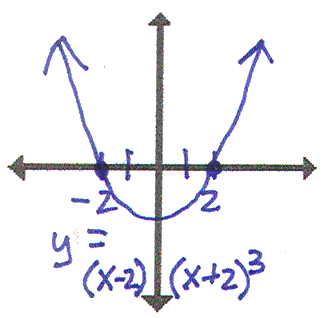 |
I have y=(x-2)(x+2)3. Who has the second degree polynomial with roots of ± 2i? |
 |
I have y=x2 + 4. Who has this polynomial translated down 4? |
 |
I have y=x2. Who has the vertex of this? |
 |
I have (0,0). Who has a concave-up quartic with this intercept and also (-2,0) and (4,0)? |
 |
I have y=x2(x+2)(x-4). Who has the reflection of this about x=0? |
 |
I have y=x2(x-2)(x+4). Who has this with a double root at x=2? |
 |
I have y=x2(x-2)2(x+4). Who has this without the roots at x=0? |
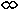 as x goes to -
as x goes to -
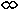 , and a double root at x=2 added?
, and a double root at x=2 added?