"Two Keys to Solving Area and Word Problems" "Resources"
|
| Summarize the Problem in Code
The semi/pseudo code looks like this and is "half symbols, half words." 50 - 3(notebooks) - 2(CDS) (first) + 3(second) + 4(third) = 131 Use the semi/pseudo code for the following reasons:
Here are the rules:
|
| Of and And, Very Important Signals
In math, as in English, AND is a signal that at least two ideas are involved. Very often these ideas also involve addition, but not always. In math, as in English, OF is a signal that information about 1 item is going to be stated. Here are expressions/equations involving of and/or and.
Below is a partial list, with mathematical symbols, of operations/ functions which require information provided through an of prepositional phrase.
The preposition "of" also acts to nest or arrange information. See how the meaning of the phrase below are changed with the arrangement of the "of." 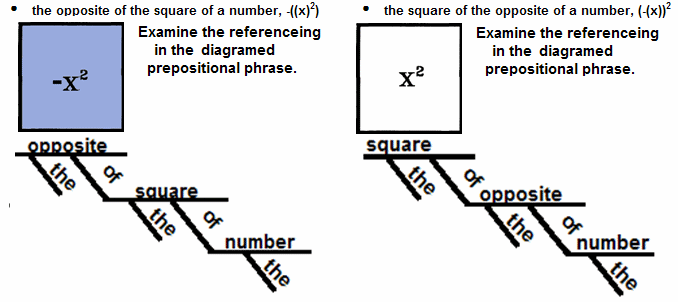 |
| Complete Example 3.
Write the code and the equation and compute the area.
|
NJCCCS
|
| Order of Operations: Math Syntax
Order of Operations is literally the order in which operations are to be performed. The rules are understood by all who write and speak mathematics.
 Restated it's: Functions, Parentheses first, next Roots or Exponents, then Multiply or Divide (left to righ) then Add or Subtract (left to right): Finally Please, Readily Excuse, My Dear Aunt Sally. Restated in a more complete form math syntax is "FIRE My Dear Aunt Sally!" In formal language, top priority first, Functions, Parentheses (and other marks of inclusing, innermost first), next Roots or Exponents (easier first), then Multiplication or Division (leftmost first), then Addition or Subtraction (leftmost first). Here's a picture or gif file. Here's a 26-page tutorial on Order of Operations. Here's are two connect the dot puzzles: 1, and 2 and their answers 1 answers and 2 answers. Here's extra problems and solutions. |
Debrief
 Lecture Notes
0
1
2
3
4
5
6
Lecture Notes
0
1
2
3
4
5
6
|
This Material Is From
|
![[master list of all MSH! dictionary words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)

![[Good Stuff -- free & valuable resources]](http://www.mathnstuff.com/gif/goods.gif)

![[MC,i. Home, site home page]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)



www.mathnstuff.com/papers/amtnj13.htm © 2013, A. Azzolino |


 ( )
( ) 