Hi,

 

Today you will:

1. Compute a z-score.
2. Compute a raw score given mean, standard deviation, and z-scores.
3. Compute a weighted mean.
4. Compute a standard deviation.
5. State probability truths in words and symbols.
6. Hand in work to the prof.

      In high school your teachers graded your tests and placed a grade on the top, or, placed a fraction on the paper to indicate how well you'd performed. That fraction is on your paper. Find the fraction with a denominator of 136, the number of points possible on the test, and compute your percent correct.

      Is that the grade on the test? Yes, for now.

      In high school you probably asked, how'd everyone else do? In some high schools the teacher would be permitted to tell you and in others this was against school policy. The mean, average, on the test was 41.333, 41.333 correct out of 136! The standard deviation was 17.5499, that's 17.5499 correct out of 136.

      In high school you knew enough to see if you were above the mean or below. It's likely you've already thought of that and know if you were above or below. You know if your performance was above average or below average. Let's call the above the mean grades positive and the below the mean grades negative. This will work well with the statistics you a to learn in the course.

      So how far above or below the mean was your grade? It's possible but not likely your grade was exactly on the mean. Take your grade and subtract the mean to give you the difference between your score and the mean.

      Compute: x - .

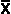      That's as far as your high school statistical analyis would probably take you.

      Complete the college version of the same analysis. Compute your z-score.

      Compute: .

      Compute the difference between your score and the mean expressed in terms of the spread of scores, the standard deviation.

      If a test is curved, according to my grading policy grades below 1 standard from the mean, z scores below -1, get an F.

      You should now be able to compute a z-score given a raw score or data point, the mean, the standard deviation.

      Test your self to see if you can do this. Make up your own numbers and use the web page to verify your computation.

(Enter negative two as "-2.")       score, x:       mean, :       standard deviation, s:       the mean from the score.       the (x - ) by s

To compute z, use the formula

      Suppose you wished to know what grade on a curved test would get you a B or an A. You would need to use the mean and the standard deviation and the z-score of 1.

      You would need to solve the equation

      Test your self to see if you can do this. Make up your own numbers and use the web page to verify your computation. The mean for this test was 41.333 and the standard deviation was 17.5499.

(Enter negative two as "-2.")       z-score, z:       mean, :       standard deviation, s:       the z-score and standard deviation.       + zs

To compute x use the formula:

      Weighted mean is the the quotient of the sum of the products of the midpoints and frequencies and n.

      It is important in itself and in other formulas.

4. Create a histogram and frequency polynomial on paper.

      Use this data.

5. Probability notes. 5. Use Chebychev's Formula and the spreadsheet to compute the percent of scores within 2, 3, 4, or some number of standard deviations of the mean.

Probability

event = result of an experiment
sample space = all the possible results of an experiment

P(event) = f/n
Sum of all probabilities = 1.  
	Every possibility must be accounted for.  
	The sum of all the fractions is 1.
	P(event1) + P(event2) + P(event3) + ... + P(eventn) = 1
P(event that can not occur) = 0
P(event that must occur) = 1
0< P(event) < 1
   _                 _

P(A) + P(not A) = 1
1 - P(A) = P(not A)
1 - P(not A) = P(A)

P(A or B) = P(A) + P(B) - P(A and B)

6. Prepare for the Test, including preparation of the Cheat Sheet. 7. Hand in work to the prof.

© A. Azzolino February 24, 2010 www.mathnstuff.com/math/spoken/here/2class/90/slab4.htm