



| Vector Addition |
|
A vector is not just a number. A vector is a number with direction. Even the symbol for a vector is different from that of a number. The symbol for a vector is a capitol letter with a ray above it. Two pieces of information are required to describe a vector -- its maginitude (size) and its direction (tilt). 
This information may be stated graphically or algebraically. When
stated algebraically vectors may be given in either rectangular form,
(x,y), or polar form, r

 , says: , says:
|
|
Simultaneously thinking magnitude, direction, x-component, y-component is the key to vector computation. Simultaneously think both polar form and rectangular form. The table below provides some simple exercises. Mentally determine the answers. If this is not possible, draw the vector. Press "=" then the other "=" to see the answers. |
R

 | (x,y) | Answers | |
| If you wish more practice or to experiment with vectors which do not lie on the axes, see graphing calculator computation, below, and get out your calculator. Graphing calculators have built in functions to change vectors (and complex numbers) from rectangular to polar and polar to rectangular forms. |
|
If you understand vector notation, it is often possible to add vectors mentally. Graphic addition permits one to see why mental addition is possible and why algebraic addition through components works so nicely. To add vectors graphically, make a head-to-tail trail, then draw a short-cut arrow to connect the start to the finish. The magnitude and direction of the short-cut arrow are the necessary symbols for the answer.
If vectors are not added graphically, they may be added mentally or algebraically. In algebraic computation of the sum of vectors, components are required. Each vector named by maginitude (size) and direction (tilt), polar coordinates, is restated relative to a rectangular coordinate system using, for two-space. x- and y-coordinates, (x,y). |
| Add the vectors or state the resultant. Check answers. | |
| | |
|
For other vector additions, sine and cosine are needed. Take the magnitude and direction of each vector and rewrite each in terms of the horizontal and vertical vectors, the x-component and y-component. Once this is done, all horizontal and vertical vectors are added and the resultant horizontal and vertical vectors are used with the inverse tangent to find the resultant direction of the vector. The horizonal and vertical vectors are then used with the Pythagorean Theorem to find the magnitude of the resultant. CHECK IT OUT IN STEPS BELOW. The graphic below dislays work. The table below that will complete computation for the reader. 
|
| 1st: Enter the magnitude and direction (in degrees) of each vector or go to the 2nd step. | |
| 2nd: Type in the x- and
y-component of each vector or press "=" to compute the x- and y-component of each vector enter in the 1st step. Note: Ax is A(cos(theta)), Ay is A(sin(theta)). |
|
| 3rd: Add the x-components to compute Rx, the x-component of the resultant. | |
| 4th: Add the y-components to compute Ry, the y-component of the resultant. | |
| 5th: Use (Rx, Ry), the x- and y-components of the resultant to determine the quadrant of the resultant. | 5th: |
| 6th: Compute theta, the direction angle, and edit
according to the signs of x and y, see step 5. Note: tan(theta)= (y/x)
| |
7th: Compute R, the magnitude of the resultant. Note:
R =
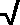 (Rx2 + Ry2) (Rx2 + Ry2)
| |
| 8th: Round as required in the situation. |
|

In math, vectors are written as (x,y) or r
On the TI-85, -86 or -89, they are written as [x,y] or [r
The symbols [ and ] are above the symobls ( and ), and
the symbol
Two TI calculator functions facilitate vector computation at
the elementary level. They are "into rectangular,"
Type [2,0] + [5
If the result is [-3,0] and you wish polar notation,
press Type [2,0] + [5
|
This page is brought to you by MATHEMATICAL CONCEPTS, inc., publishers of MATH SPOKEN HERE!, ISBN: 0-9623593-5-1.
You are hereby granted permission to make ONE printed copy of this page and its picture(s) for your PERSONAL and not-for-profit use. YOU MAY NOT MAKE ANY ADDITIONAL COPIES OF THIS PAGE, ITS PICTURE(S), ITS SOUND CLIP(S), OR ITS ANIMATED GIFS WITHOUT PERMISSION FROM: classes@mathnstuff.com or by mail to the address below.

|