
The Visual / Auditory / Symbolic / Kinesthetic Approach to Algebra

Fraction Bars are a better manipulative than Term Tiles for introducing multiples, equivalent fractions, and addition or subtraction of arithmetic fractions. Term Tiles are a better manipulatives than Fraction Bars when it comes to representing or computing with algebraic fractions. To write an equivalent fraction:
Below, what looks like a piece of a times table, a 3-strip or multiples-of-3-strip is pictured. In boxes the three times tables is displayed from left to right, smallest to largest. It is not an infinite strip so only the smallest multiples of 3 are printed in the boxes. 
Below, a 3-strip is paired with a 4-strip to create, in Numerator / Denominator Display, a 3/4-strip. It shows the smallest multiples of three-fourths and in this three-fourths-stip, one can see that the fractions 6/8, 9/12, 12/16, all reduce to 3/4. 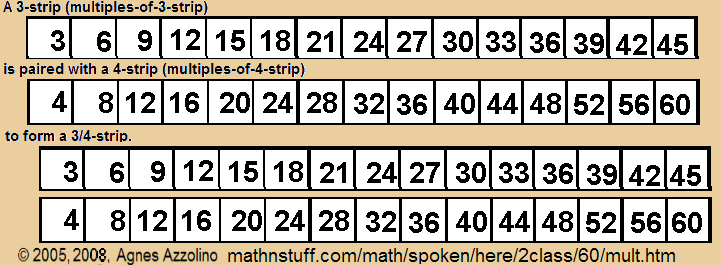
Writing equivalent fractions looks a lot like reducing fractions. Writing equivalent fractions and reducing fractions are inverses. One involves making multiples in the numerator and denominator, the other involves factoring out the common multiple in both the numerator and denominator. Identical rows are used to both reduce and write equivalent fractions. 
In the Tilted Tile Display of 6/10, and 9/15, note the identical row of tiles. Each fraction may be reduced to the 3/5, the ratio depicted in one row. The fraction 3/5 may be rewritten as 6/10, or 9/15, or 12/20, or 15/25,… If the desired denominator is 12, the required numeration is 9 1/5, and, this can not be represented manipulatively without knowledge of proportions. But, it isn't usually addressed by pencil and paper computation without proportions either. Below in the Numerator / Denominator Display of 2/(x+1) and (2(x+2))/[(x+2)(x+1)] and (2x)/(x(x+1)), it is necessary to write numerator and denominator in factored form in order to see the common factors. 
Write Equivalent Fractions in Tilted Tile Display.
Write Equivalent Fractions in Numerator / Denominator Display.
|
 
 www.termtiles.com, Unit 30 © 2008, A. Azzolino |