|
Factor - A Noun and A Verb
|
|
To
factor 12, one must find numbers which when multiplied produce twelve.
Three and four are a pair of such factors. Three and four are a
factor pair of 12.
Term Tiles and Tokens may be used to find factors and factor pairs and to
factor an expression.
 | By way of quick vocabulary review,
- The factors of 3 and 4 are represented vertically and horizontally in storage around the display area.
- Their product, 12, is represented by a rectangular array of tiles.
- Four and three are factors of
twelve. So are 1 and 12, 2 and 6, 9 and 1.5.
- The
prime factorization of 12, the expression equaling 12 composed only of
prime factors whose product is 12, is 2x2x3.
|
- Show me all the possible rectangles that have an area of 24 square units.
- Show me all the possible rectangular areas of -6 tiles and state their dimensions.
- Multiply (x+2)(x-6).
- Divide x² - x - 6 by x-3.
The tasks above set the stage for success in factoring. The tasks below exemplify the challenges of algebraic factoring.
- Factor: 3x³ + 6x² + 9x Polynomials with A Monomial Factor
- Factor: x² + 6x + 5 Trinomials -- UnFOIL
- Factor: 15x² + 11x - 12 Trinomials when the Leading Coefficient Is Not One
Factoring a common monomial is the first factoring taught in an algebra course.
It is the distributive law used to collect rather than distribute factors. It is the hardest factoring to complete
because to recognize what factors terms have in common, one must recognize the factors themselves.
Term Tiles facilitate monomial factoring because the lining up identical rows (see
Representing Fractions) is factoring a monomial.
Factoring a trinomial into two binomials is what one thinks of when completing
factoring. Most students retain this skill long after algebra I, and, that's very good because the skill is used in
algebra II and precalc and other math related courses like physics. Students know how the task is to be
completed and many know why, but, Term Tiles introduce and reinforce the algorithm extremely well.
Factoring a trinomial with a leading coefficient that is not 1 is a task some students
never achieve, even with practice with one or more algorithms. Term Tiles make this factoring a skill nearly,
if not all, can attain.
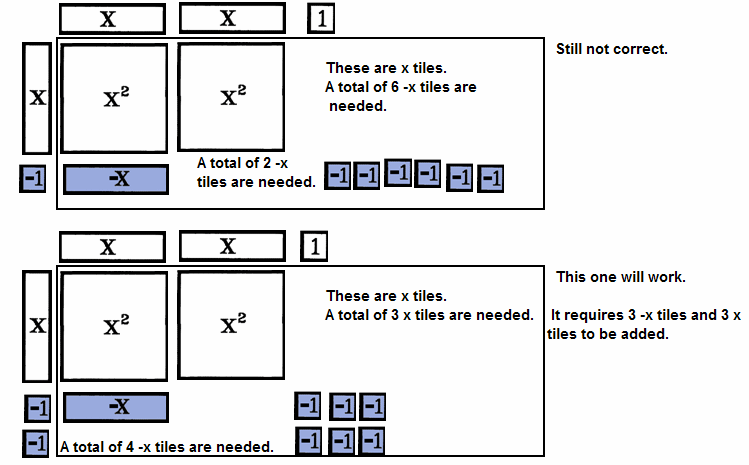
- To Factor An Expression:
| 1st: | Represent the expression in the display area in descending order with
leading terms in the upper left and constants on the right. |
| 2nd: | IF POSSIBLE, arrange the tiles in IDENTICAL horizontal rows (forming a
rectangular display area) then complete step 5. |
| 3rd: | IF IT IS NOT POSSIBLE to form identical rows, arrange the tiles with
the leading tiles in the upper left and the constants in the lower right, seeking a binomial factor.
If looking for a binomial factor, think FOIL where the F area is the x² tiles and the
L area is the constant tiles. Arrange the tiles in a rectangular array if possible. |
| 4th: | IF IT IS NOT POSSIBLE to form binomial factors with existing tiles, try
adding additional zeros to the display area, an x tile with a -x tile, as needed to complete a rectangular area
using the existing tiles. |
| 5th: | IF IT IS NOT POSSIBLE to form a rectangular area even after adding pairs
of zeros, the expression can not be factored. Skip step 6. |
| 6th: | Represent the dimensions of the rectangular area on the left in the vertical
storage area and on the top horizontal storage area. These are factors of the expression in the display
area. |
| 7th: | Record each expressions in the border storage areas then factor each
expression (mentally or manipulatively), beginning with step 1. |
| 8th: | Review EACH factor in the final expression checking to see if it can be
factored. Verify that the product of the factors is the original expression. |
Factor. Answers are shown below and individually through the arrows.
a. Factor 2x - 2 
b. Factor 3x+6 
c. Factor x²+3x 
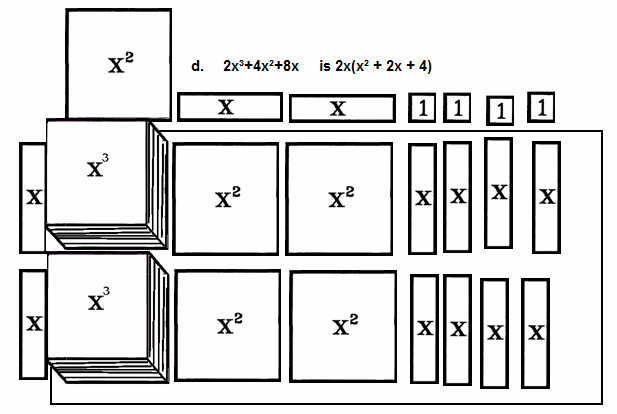
d. Factor 2x³+4x²+8x 
|
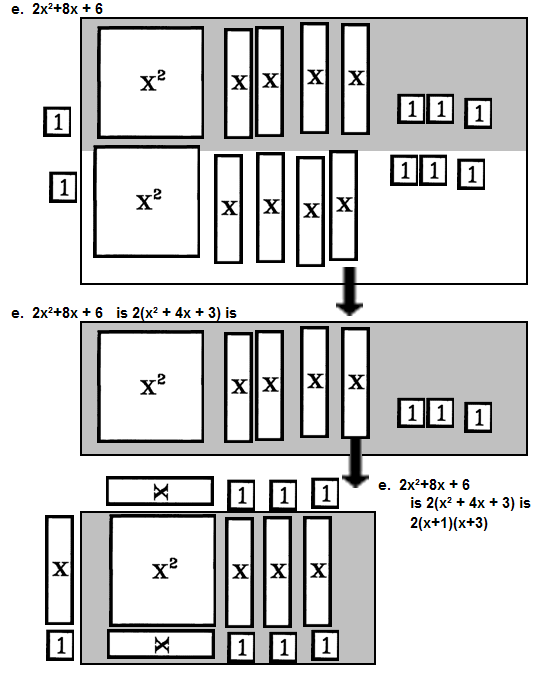
e. Factor 2x²+8x + 6

f. Factor x² + 2x +1 
g. Factor x² + 7x + 12 
h. Factor x² - 7x + 12  |
i. Factor x² - 5x + 6

j. Factor x² - 4 
k. Factor x² + x -12 
l. Factor x² - x - 12 
m. Factor 2x²-x-6 
 
 |
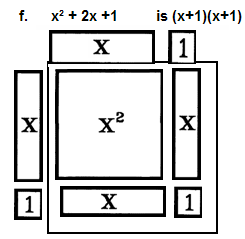 |
This is an example of "unFOILing" - factoring a trinomial into
two binomials. Notice 4 different regions, corresponding to the First, Outer, Inner, and Last products of the
multiplication of two binomials. Notice that the upper left region is the x² region, the lower right is the
constant region, and the linear or x regions are the remaining corners.
This
problem is easy because all signs are positive and, because 1 is prime, it may be factored in only one way.
|
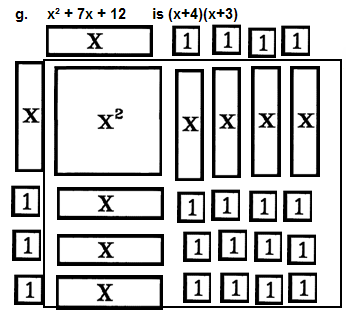 |
This problem is a bit more difficult, not because of the signs but, because 12
is composite. Twelve may be factored in more than 1 way. |
 |
This problem is a bit more difficult. The sign of the constant term is positive
and this indicates the x tiles are all the same kind. The sign on the linear, x, term is negative indicating, in
conjunction with the above, that all the x tiles are negative.
Just a brief note:
When the sign of the constant term is positive, it means that the factors were (+)(+) or (-)(-), the same. If the
sign of the constant term were negative, it means the factors were (+)(-) or (-)(+), opposites. |
 |
- Two ideas are important here.
- 1. The sign of the constant term is positive, so the linear tiles are all the same sign.
- 2. The sign of the linear term is negative so there are more -x tiles than x tiles.
|




|




















