A student who is not symbolically savy may not see a factor of -1 when reducing
a fraction. Negative 1 is a very difficult factor to see. The pictures and the analysis questions below might
facilitate understanding.
| Questions 1 - 5: |
a. How are the two representations the same? |
| | b. How are the two representation different? |
- 1. the fraction 4 ÷ - 4 and the fraction 5 ÷ - 5.
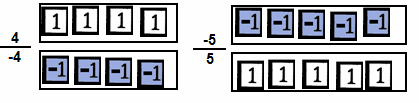 -
- 2. the fraction (x-2)/(2-x) on the left and the fraction (x-2)/(2-x) on the right.
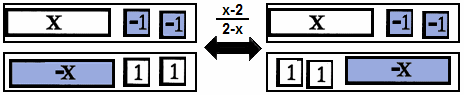 -
- 3. the fraction (x-2)/(2-x) and the fraction (3-x)/(x-3).
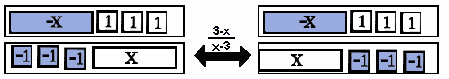 -
- 4. the (x+4)(x-2)/(x+4)(2-x) on the left and the fraction (x+4)(x-2)/(x+4)(2-x) on the right.
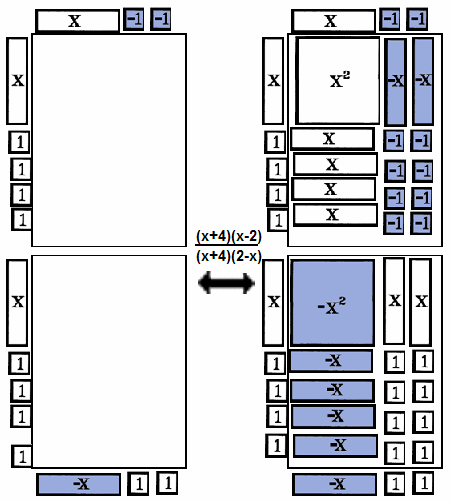 -
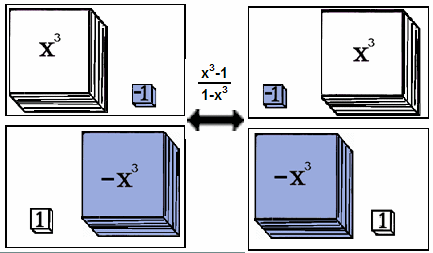
- 5. the fraction (x3-1)/(1-x3) on the left and on the right.
 -
-
- Questions 6 - 8: Reduce.
- 6. 4 ÷ -4
7. (x-2)/(2-x) 8. (x+4)(x-2)/(x+4)(2-x)
-
- Question 9: How does one recognize that a fraction is equal to -1 or has -1 as a factor?
| Why Is (a-b)/(b-a) Equal to -1?
| |
Before reviewing answers to the questions, recall the reason (a-b)/(b-a) is equal
to -1. First, symbolic multiplication, distributing, is reviewed, after that, the fraction is reduced by the
algorithm listed farther below on the page.
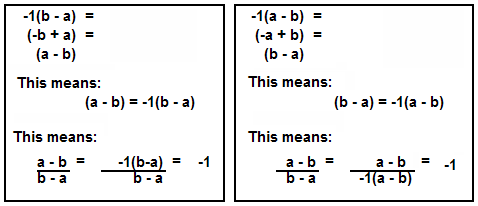

It doesn't matter whether the part of the fraction that is factored is the top or
the bottom. The factored part is always the product of -1 and the other fraction part. Since the matching top
factor divided by the matching bottom factor reduces to 1, the factor that is left, -1, is the result.
| Some Answers to Questions
| |
| Questions 1 - 5: |
a. How are the two representations the same? |
| | b. How are the two representation different? |
- 1. the fraction 4 ÷ - 4 and the fraction 5 ÷ - 5.
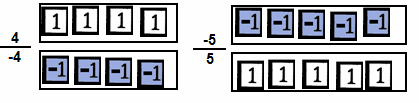
same
- They each have the same number of tiles on the top and the bottom.
- They are all constant tiles.
- The tiles on the bottom are a different colors from those on the top.
- The top and bottom are opposites.
different
- One has bunches of 4 or -4 tiles and the other has bunches of 5 or -5.
-
- 2. the fraction (x-2)/(2-x) on the left and the fraction (x-2)/(2-x) on the right.

same
- Same two terms on the top as on the bottom.
- Each has two kinds of terms or tiles.
- Each numerator and denominator has 4 tiles -- 2 constant tiles, 2 linear tiles.
- It's "half" blue and "half" white on the top and the bottom.
- The tops are the same. The bottoms have tiles in different positions.
- The blue (negative) tiles and the white (positive) tiles switch on the top and bottom.
different
- The tops are the same. The bottoms have tiles in different positions.
-
- 3. the fraction (x-2)/(2-x) and the fraction (3-x)/(x-3).
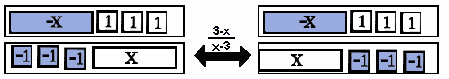
same
- Each has x and -x on the top and on the bottom.
- Each has two kinds of terms or tiles.
different
- One has 2 and -2 and the other has 3 and -3.
- With the top of (x-2)/(2-x) the positive terms is first and the negative terms are second and it's the
other way with the other fraction.
-
- 4. the (x+4)(x-2)/(x+4)(2-x) on the left and the fraction (x+4)(x-2)/(x+4)(2-x) on the right.

same
- Each product has a column of blues and a column of whites.
- The vertical factors are the same.
- Each horizontal factor has two kinds of tiles.
different
- The columns of blues and whites are switched.
- The horizontal factors are different. They're opposites.
-
- 5. the fraction (x3-1)/(1-x3) on the left and on the right.

same
- They are cubic tokens.
- Each has two kinds of tokens- variable and constants.
different
- On the left the column of whites is on the left and on the right the whites are on the right.
-
- Questions 6 - 8: Reduce.
- 6. 4 ÷ -4 = -1
7. (x-2)/(2-x) = -1 8. (x+4)(x-2)/(x+4)(2-x) = -1
-
- Question 9:
- How does one recognize that a fraction is equal to -1 or has -1 as a factor?
- Look for switched blues and whites, negatives and positives, on the tops and bottoms.
- Look for one or two kinds of tiles.
- If the top is the opposite of the bottom, the fraction is equal to -1.
In question 5, the fraction (x3-1)/(1-x3) is examined.
The fraction is equal to -1.
This is not for most students! It may "make your eyes hurt." Take it slow,
step by step, numerator first, then denominator, then both numerator and denominator.
This is not for all students. Think "derive the quadratic formula by completing
the square." It's a task usually reserved for the teacher. Most likely "reducing a rational expression
involving cubics" is also reserved for the teacher. It is provided here in graphic form.
Ok, so the plan is to represent the fraction, then factor the numerator,
factor the denominator, then work on both the numerator and denominator to reduce the fraction.
So one's "eyes don't hurt" each piece is isolated in graphic form and a printable copy is provided below
the symbolic answer.
- 1st: Represent the fraction.
 Use Numerator / Denominator Format. Use Numerator / Denominator Format.

 Begin to factor based on the given terms / tiles / tokens. Begin to factor based on the given terms / tiles / tokens.
Here the vertical factor names the height of the
term/tile/token and the horizontal factor represents the base. 
-
- 2nd: Factor the numerator.
 Use appropriate "zero pairs" to fill in the rectangular area. Use appropriate "zero pairs" to fill in the rectangular area.
 Determine what "zero pair" is need by completing the multiplication
given the known terms/tiles/tokens and their factors. Determine what "zero pair" is need by completing the multiplication
given the known terms/tiles/tokens and their factors.

 Keep the factored terms and factor parts in the current
position. Keep the factored terms and factor parts in the current
position.
Move the "extra" terms from the "zero pairs" to an empty position and
continue the factoring (if possible).
Thinking "height times base" won't work
now, so, just think, "What times this gives me this?" 
-
- 3rd: Factor the denominator.

 
-
- 4th: Work on both numerator and denominator to reduce the fraction.

 Remember: Remember:-
TO REDUCE, USE THE
FACTORS
THEY DON'T HAVE IN COMMON
AS THE NEW NUMERATOR AND THE NEW DENOMINATOR.
|
 The horizontal factors are common to numerator and denominator. The horizontal factors are common to numerator and denominator.
They reduce to 1 and need not be used. Use the vertical factors.
 
- 5th: Repeat the process.
 Factor. Reduce using factors NOT IN COMMON in the reduced
fraction. Factor. Reduce using factors NOT IN COMMON in the reduced
fraction. 

Using algebraic symbols, the work is easier IF on knows how to factor a cubic. With tiles,
one need not used a formula but rather a procedure used with rational numbers with quadratic polynomials.

A printable copy is provided.
|




